题目内容
如图，已知A是半径为1的⊙O上一点，以A为圆心，AO为半径画弧交⊙O于点B、C；以C为圆心，CO为半径画弧交⊙O于点D、A．则图中阴影面积为分析：连接AB，AO，OC，CD，将问题转化为圆的面积-3个扇形的面积-2个弓形的面积．
解答：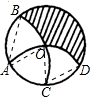
解：如图，连接AB，AO，OC，CD，
依题意，得∠BAO=∠AOC=∠OCD=60°，
∴S阴影部分=S⊙O-S扇形BAO-S扇形AOC-S扇形OCD-S弓形AB-S弓形CD
=π-3×
-2×（
-
）
=
π+
．
故答案为：
π+
．
解：如图，连接AB，AO，OC，CD，依题意，得∠BAO=∠AOC=∠OCD=60°，
∴S阴影部分=S⊙O-S扇形BAO-S扇形AOC-S扇形OCD-S弓形AB-S弓形CD
=π-3×
| 60×π×12 |
| 360 |
| 60×π×12 |
| 360 |
| ||
| 4 |
=
| 5 |
| 6 |
| ||
| 2 |
故答案为：
| 5 |
| 6 |
| ||
| 2 |
点评：本题考查了扇形的面积计算．关键是利用割补法将图形分割为几个基本图形求面积的和差关系．
练习册系列答案
相关题目
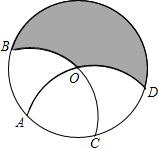如图，已知A是半径为1的⊙O上一点，以A为圆心，AO为半径画弧交⊙O于点B、C；以C为圆心，CO为半径画弧交⊙O于点D、A，则图中阴影面积为
14、如图，已知AB是半径为1的圆O的一条弦，且AB＜1，以AB为一边在圆O内作正△ABC，点D为圆O上不同于点A的一点，且DB=AB，DC的延长线交圆O于点E，试探究AE的长是否为定值（不随AB长度的变化而变化）？若为定值，求出这个定值；若不为定值，试确定AE与AB长之间的关系．
