题目内容
【题目】已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.

(1)求证:DE为⊙O的切线.
(2)求证:AB:AC=BF:DF.
【答案】详见解析
【解析】
(1)连接OD、AD,求出CDA=∠BDA=90°,求出∠1=∠4,∠2=∠3,推出∠4+∠3=∠1+∠2=90°,根据切线的判定推出即可;
(2)证△ABD∽△CAD,刘![]() ,证△FAD∽△FDB,得
,证△FAD∽△FDB,得![]() ,即可得出AB:AC=BF:DF。
,即可得出AB:AC=BF:DF。
证明:(1)连接DO、DA,
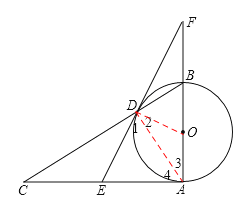
∵AB为⊙O直径,∴∠CDA=∠BDA=90°。
∵CE=EA,∴DE=EA。∴∠1=∠4。
∵OD=OA,∴∠2=∠3。
∵∠4+∠3=90°,∴∠1+∠2=90°,即:∠EDO=90°。
∴DE⊥OD。
∵OD是半径,∴DE为⊙O的切线。
(2)∵∠3+∠DBA=90°,∠3+∠4=90°,
∴∠4=∠DBA。
∵∠CDA=∠BDA=90°,∴△ABD∽△CAD。
∴![]() 。
。
∵∠FDB+∠BDO=90°,∠DBO+∠3=90°,
又∵OD=OB,∴∠BDO=∠DBO。∴∠3=∠FDB。
∵∠F=∠F,∴△FAD∽△FDB。∴![]() 。
。
∴![]() ,即AB:AC=BF:DF。
,即AB:AC=BF:DF。

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
【题目】在济南市开展的“美丽泉城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成不完整的统计图表,如图所示:
劳动时间(时) | 频数(人数) | 频率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.4 |
2 | 18 | y |
合计 | m | 1 |
(1)统计表中的x= ,y= ;
(2)被调查同学劳动时间的中位数是 时;
(3)请将频数分布直方图补充完整;
(4)求所有被调查同学的平均劳动时间.