题目内容
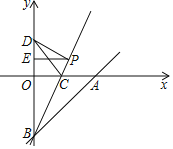
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF.
(1)求证:四边形AECF是菱形;
(2)若AC=4,BE=1,直接写出菱形AECF的边长.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据正方形的性质和菱形的判定解答即可;
(2)根据正方形和菱形的性质以及勾股定理解答即可.
(1)证明:∵正方形ABCD的对角线AC,BD相交于点O,
∴OA=OC,OB=OD,
AC⊥BD.
∵BE=DF,
∴OB+BE=OD+DF,即OE=OF.
∴四边形AECF是平行四边形.
∵AC⊥EF,
∴四边形AECF是菱形.
(2)∵AC=4,
∴OA=2,
∴OB=2,
∴OE=OB+BE=3,

练习册系列答案
相关题目