题目内容
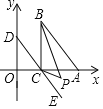
【题目】如图，矩形ABCD的面积为20cm2，对角线相交于点O．以AB、AO为邻边画平行四边形AOC1B，对角线相交于点O ；以AB、AO 为邻边画平行四边形AO1C2B，对角线相交于点O2 ：……以此类推，则平行四边形AO4C5B的面积为（ ）
A.
cm2B.
cm2C.
cm2D. 
cm2
【答案】A
【解析】
设矩形ABCD的面积为S=20cm2，由O为矩形ABCD的对角线的交点，可得平行四边形AOC1B底边AB上的高等于BC的
，依此类推可得下一个图形的面积是上一个图形的面积的，然后求解即可．
设矩形ABCD的面积为S=20cm2，
∵O为矩形ABCD的对角线的交点，
∴平行四边形AOC1B底边AB上的高等于BC的，
∴平行四边形AOC1B的面积=S，
∵平行四边形AOC1B的对角线交于点O1，
∴平行四边形AO1C2B的边AB上的高等于平行四边形AOC1B底边AB上的高的，
∴平行四边形AO1C2B的面积=×S=
，
……
依此类推，平行四边形AO4C5B的面积=
=
=
（cm2），
故选：A．
练习册系列答案
相关题目
