题目内容
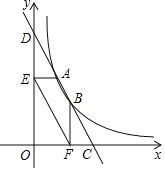
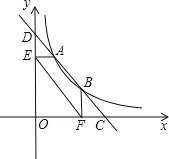
【题目】直线y=﹣2x+5分别与x轴,y轴交于点C、D,与反比例函数y=![]() 的图象交于点A、B.过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,连结EF;下列结论:①AD=BC;②EF∥AB;③四边形AEFC是平行四边形;④S△EOF:S△DOC=3:5.其中正确的个数是( )
的图象交于点A、B.过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,连结EF;下列结论:①AD=BC;②EF∥AB;③四边形AEFC是平行四边形;④S△EOF:S△DOC=3:5.其中正确的个数是( )
A. 1B. 2C. 3D. 4
【答案】C
【解析】
①先把反比例函数、一次函数解析式联合组成方程组,解可求A、B坐标,根据y=﹣2x+5可求C、D的坐标,而AE⊥y轴,BF⊥x轴,结合A、B、C、D的坐标,可知AE=1,DE=OD﹣OE=5﹣3=2,在Rt△ADE中利用勾股定理可求AD=![]() ,同理可求BC=
,同理可求BC=![]() ,于是AD=BC,①正确;
,于是AD=BC,①正确;
②根据A、B、C、D的坐标,易求OF:OE=1:2,OC:OD=1:2,即OF:OE=OC:OD,斜率相等的两直线平行,那么EF∥AB,故②正确;
③由于AE=CF=1,且AE∥CF,根据一组对边相等且平行的四边形是平行四边形,可知四边形AEFC是平行四边形,故③正确;
④根据三角形相似的性质可求得求S△EOF:S△DOC=9:25,故④错误.
如图所示,
①解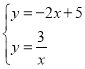 ,得
,得![]() 或
或![]() ,
,
∴A点坐标是(1,3),B点坐标是(![]() ,2),
,2),
∵直线y=﹣2x+5与x轴和y轴的交点分别是(![]() ,0)、(0,5),
,0)、(0,5),
∴C点坐标是(![]() ,0),D点坐标是(0,5),
,0),D点坐标是(0,5),
∵AE⊥y轴,BF⊥x轴,
∴AE=1,DE=OD﹣OE=5﹣3=2,
在Rt△ADE中,AD=![]() =
=![]() ,
,
同理可求BC=![]() ,
,
故AD=BC,
故①选项正确;
②∵OF:OE=1:2,OC:OD=1:2,
∴EF∥AB,
故②选项正确;
③∵AE=CF=1,且AE∥CF,
∴四边形AEFC是平行四边形,
故③选项正确;
④∵EF∥CD,
∴△EOF∽△DOC,
∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,故④选项错误.
,故④选项错误.
故选:C.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案