题目内容
(1)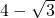 的整数部分为a,小数部分为b,求a-b的值.
的整数部分为a,小数部分为b,求a-b的值.
(2)已知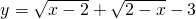 ,求yx.
,求yx.
解:(1)∵1<3<4,
∴1< <2,
<2,
∴2<4- <3,
<3,
∴a=2,b=4- -2=2-
-2=2- ,
,
∴a-b=2-(2- )=2-2+
)=2-2+ =
= ;
;
(2)根据题意得,x-2≥0且2-x≥0,
解得x≥2且x≤2,
∴x=2,
y=-3,
∴yx=(-3)2=9.
分析:(1)根据 大于1小于2可知4-
大于1小于2可知4- 在2到3之间,然后求出a、b的值,再代入代数式进行计算即可求解;
在2到3之间,然后求出a、b的值,再代入代数式进行计算即可求解;
(2)根据二次根式有意义的条件,被开方数大于等于0列式求出x的取值范围并解得x的值,然后求出y的值,代入代数式进行计算即可求解.
点评:本题考查了无理数的估算与二次根式有意义的条件,(1)中“夹逼法”是估算无理数的大小常用的方法,(2)根据被开方数大于等于0得到x的值是解题的关键.
∴1<
 <2,
<2,∴2<4-
 <3,
<3,∴a=2,b=4-
 -2=2-
-2=2- ,
,∴a-b=2-(2-
 )=2-2+
)=2-2+ =
= ;
;(2)根据题意得,x-2≥0且2-x≥0,
解得x≥2且x≤2,
∴x=2,
y=-3,
∴yx=(-3)2=9.
分析:(1)根据
 大于1小于2可知4-
大于1小于2可知4- 在2到3之间,然后求出a、b的值,再代入代数式进行计算即可求解;
在2到3之间,然后求出a、b的值,再代入代数式进行计算即可求解;(2)根据二次根式有意义的条件,被开方数大于等于0列式求出x的取值范围并解得x的值,然后求出y的值,代入代数式进行计算即可求解.
点评:本题考查了无理数的估算与二次根式有意义的条件,(1)中“夹逼法”是估算无理数的大小常用的方法,(2)根据被开方数大于等于0得到x的值是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目