题目内容
（2012•河东区二模）如图，已知AD是圆O直径，点C在圆上，点B在线段AD延长线上，且∠A=∠B=30°，连接BC．（1）证明：BC是圆O的切线；
（2）若圆O的半径为
| 3 |
分析：（1）连接OC．欲证BC是圆O的切线，只需证明BC⊥OC；
（2）连接CD．通过相似三角形△BDP∽△BCO的对应边成比例列出比例式
=
，从而求得PD的长度．
（2）连接CD．通过相似三角形△BDP∽△BCO的对应边成比例列出比例式
| PD |
| OC |
| BD |
| BC |
解答：
（1）证明：连接OC．
∵∠A=∠B=30°，
∴∠ACB=120°，
又∵OA=OC，
∴∠ACO=∠A=30°，
∴∠BCO=∠ACB-∠ACO=90°，
∴BC⊥OC，
∴BC是圆O的切线；
（2）解：连接CD．
∵∠BCD=∠ACB-∠ACD=120°-90°=30°，
∴∠BCD=∠B，
∴DB=DC．
又∵在Rt△ACD中，DC=AD•sin30°=
，
∴BD=
，
∵直线DP为圆O的切线，
∴DP⊥AB，则△BDP∽△BCO，
∴
=
，
∵BC=
=3，
∴PD=
×OC=
×
=1．
（1）证明：连接OC．∵∠A=∠B=30°，
∴∠ACB=120°，
又∵OA=OC，
∴∠ACO=∠A=30°，
∴∠BCO=∠ACB-∠ACO=90°，
∴BC⊥OC，
∴BC是圆O的切线；
（2）解：连接CD．
∵∠BCD=∠ACB-∠ACD=120°-90°=30°，
∴∠BCD=∠B，
∴DB=DC．
又∵在Rt△ACD中，DC=AD•sin30°=
| 3 |
∴BD=
| 3 |
∵直线DP为圆O的切线，
∴DP⊥AB，则△BDP∽△BCO，
∴
| PD |
| OC |
| BD |
| BC |
∵BC=
| BO2-CO2 |
∴PD=
| BD |
| BC |
| ||
| 3 |
| 3 |
点评：本题考查了切线的判定与性质、相似三角形的判定与性质．判定切线时，经常作的辅助线是“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”．
练习册系列答案
相关题目
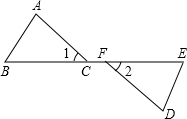（2012•河东区二模）如图，点B，C，F，E在同一直线上，∠1=∠2，BC=FE，要使△ABC≌△DEF，还需添加一个条件，这个条件可以