Question

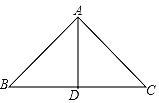
【题目】如图，在四边形ABCD中，AC平分∠BAD，AD=AC，在AC上截取AE=AB，连接DE、BE，并延长BE交CD于点 F，以下结论：①△BAC≌△EAD；②∠ABE+∠ADE=∠BCD；③BC+CF=DE+EF；其中正确的有（ ）个

A. 0 B. 1 C. 2 D. 3

Answer 1

【答案】D

【解析】

通过SAS可证明△BAC≌△EAD，即可判断①；由等腰三角形的性质及三角形内角和定理可得出∠ABE=∠ACF，再由全等三角形对应角相等得出∠ACB=∠ADE，即可判断②；通过证明∠FEC=∠FCD，得到EF=CF，再由全等三角形对应边相等得出BC=ED，即可判断③．

∵AC平分∠BAD，∴∠BAC=∠DAC．

在△BAC和△EAD中，∵AB=AE，∠BAC=∠DAC，AC=AD，∴△BAC≌△EAD，故①正确；

设∠BAC=x，则∠DAC=x．

∵AB=AE，∴∠ABE=∠AEB=．

∵AC=AD，∴∠ACD=∠ADC=，∴∠ABE=∠ACF．

∵△BAC≌△EAD，∴BC=ED，∠ACB=∠ADE，∴∠ABE+∠ADE=∠ACD+∠ACB=∠BCD，故②正确；

∵∠ABE=∠AEB=∠ACD，∠FEC=∠AEB，∴∠FEC=∠FCD，∴EF=CF．

∵BC=ED，∴BC+CF=DE+EF，故③正确．

故选D．