题目内容
【题目】如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:四边形BCEF是平行四边形.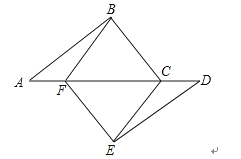
【答案】证明:在△AFB和△DCE中,
∴△AFB≌△DCE(SAS),
∴FB=CE,
∴∠AFB=∠DCE,
∴FB∥CE,
∴四边形BCEF是平行四边形.
【解析】首先证明△AFB≌△DCE(SAS),进而得出FB=CE,FB∥CE,进而得出答案.
【考点精析】通过灵活运用平行四边形的判定,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形即可以解答此题.

练习册系列答案
相关题目
【题目】用火柴棒按下列方式搭建三角形:
![]()
(1)填表:
三角形个数 | 1 | 2 | 3 | 4 |
图火柴棒根数 | 3 |
|
|
|
(2)当有n个三角形时,应用多少根火柴棒?(用含n的代数式表示);
(3)当有2017根火柴棒时,照这样可以摆多少个三角形?