题目内容
如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
甲、乙、丙、丁四人进行射击测试,每人测试10次,平均成绩均为9.2环,方差如表所示
选手 | 甲 | 乙 | 丙 | 丁 |
方差 | 0.56 | 0.60 | 0.50 | 0.45 |
则在这四个选手中,成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁


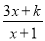 的值为零,则k=__________.
的值为零,则k=__________.
 ,tan∠A=
,tan∠A= ,求AE的长.
,求AE的长.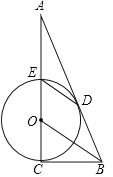
 ,则x取值范围是_____.
,则x取值范围是_____.