题目内容
同学们,折纸中也有很大的学问呢.张老师出示了以下三个问题,小聪、小明、小慧分别在黑板上进行了板演,请你也解答这个问题:
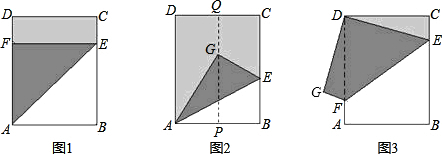
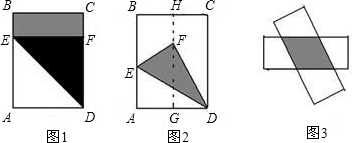
在一张长方形ABCD纸片中,AB=25cm,AD=20cm,现将这张纸片按下列图示方法折叠,请解决下列问题.
(1)如图1,折痕为DE,点A的对应点F在CD上,则折痕DE的长为______;
(2)如图2,H,G分别为BC,AD的中点,A的对应点F在HG上,折痕为DE,求重叠部分的面积;
(3)如图3,在图2中,把长方形ABCD沿着HG对开,变成两张长方形纸片,将两张纸片任意叠合后,发现重叠部分是一个菱形,显然,这个菱形的周长最短是40cm,求叠合后周长最大的菱形的周长和面积.
解:(1)∵四边形ADFE是正方形,
∴DE=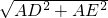 =
= =20
=20 cm;
cm;
(2)由折叠的性质可知,AD=DF,
∵GH分别是AD、BC的中点,
∴GD= AD=
AD= DF
DF
∴在Rt△DGE中,∠GFD=30°,∠GDF=60°,
∵∠GDE=∠EDF,
∴∠EDA=30°.
∴在Rt△ADE中,tan∠EDA=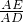 ,
,
∴AE=AD•tan30°=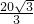
∴S△DEF= AE•AD=
AE•AD= ×20×
×20×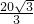 =
=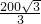 ;
;
 (3)最大的菱形如图所示:
(3)最大的菱形如图所示:
设GK=x,则HK=25-x,
x2=(25-x)2+102,
解得x=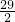 ,
,
则菱形的周长为58cm,
此时菱形的面积S=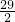 ×10=145.
×10=145.
分析:(1)根据图形折叠的性质可知AD=AE=20cm,再根据勾股定理即可得出结论;
(2)由折叠的性质可得到DG= AD=
AD= DE,再根据直角三角形的性质得出∠EDA=30°,由锐角三角函数的定义得到AE的长,利用三角形的面积公式即可得出结论;
DE,再根据直角三角形的性质得出∠EDA=30°,由锐角三角函数的定义得到AE的长,利用三角形的面积公式即可得出结论;
(3)设GK=x,则HK=25-x,利用勾股定理即可求出x的值,进而可得出菱形的周长求出其面积.
点评:本题考查的是图形的翻折变换、菱形及矩形的性质、三角形的面积公式,熟知图形翻折变换的性质是解答此题的关键.
∴DE=
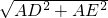 =
= =20
=20 cm;
cm;(2)由折叠的性质可知,AD=DF,
∵GH分别是AD、BC的中点,
∴GD=
 AD=
AD= DF
DF∴在Rt△DGE中,∠GFD=30°,∠GDF=60°,
∵∠GDE=∠EDF,
∴∠EDA=30°.
∴在Rt△ADE中,tan∠EDA=
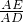 ,
,∴AE=AD•tan30°=
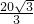
∴S△DEF=
 AE•AD=
AE•AD= ×20×
×20×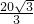 =
=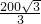 ;
; (3)最大的菱形如图所示:
(3)最大的菱形如图所示:设GK=x,则HK=25-x,
x2=(25-x)2+102,
解得x=
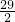 ,
,则菱形的周长为58cm,
此时菱形的面积S=
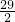 ×10=145.
×10=145.分析:(1)根据图形折叠的性质可知AD=AE=20cm,再根据勾股定理即可得出结论;
(2)由折叠的性质可得到DG=
 AD=
AD= DE,再根据直角三角形的性质得出∠EDA=30°,由锐角三角函数的定义得到AE的长,利用三角形的面积公式即可得出结论;
DE,再根据直角三角形的性质得出∠EDA=30°,由锐角三角函数的定义得到AE的长,利用三角形的面积公式即可得出结论;(3)设GK=x,则HK=25-x,利用勾股定理即可求出x的值,进而可得出菱形的周长求出其面积.
点评:本题考查的是图形的翻折变换、菱形及矩形的性质、三角形的面积公式,熟知图形翻折变换的性质是解答此题的关键.

练习册系列答案
相关题目