题目内容
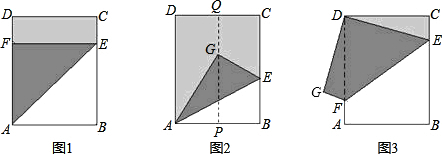
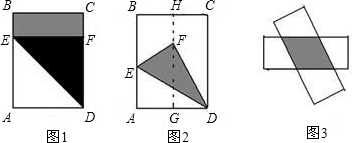
同学们,折纸中也有很大的学问呢.黄老师出示了以下三个问题,小聪、小明、小慧分别在黑板上进行了板演,请你也解答这个问题:在一张长方形ABCD纸片中,AD=25cm,AB=20cm,现将这张纸片按如下列图示方式折叠,分别求折痕的长.
(1)如图1,折痕为AE;
(2)如图2,P,Q分别为AB,CD的中点,折痕为AE;
(3)如图3,折痕为EF.

【答案】分析:本题的折叠问题由易到难,图(1)(2)都是轴对称的两个三角形,图(3)是轴对称的两个直角梯形,过F作FM⊥BC,FM就与FD对称,将问题转化求解.
解答: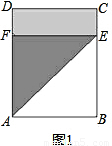 解:(1)∵由折叠可知△ABE为等腰直角三角形,
解:(1)∵由折叠可知△ABE为等腰直角三角形,
∴AE= AB=20
AB=20 cm;
cm;
(2)∵由折叠可知,AG=AB,∠GAE=∠BAE,
∵点P为AB的中点
∴AP= AB
AB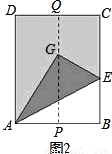
∴AP= AG
AG
在Rt△APG中,得∠GAP=60°
∴∠EAB=30°
在Rt△EAB中,AE=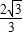 AB=
AB=
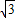 cm;
cm;
(3)解法一:连接BD,交EF于点O,
由勾股定理得:BD=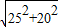 =5
=5

由折叠可知,折痕EF为BD的垂直平分线
∴OD= BD=
BD=
可证△DOF∽△DAB
∴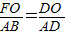
∴FO=2
由对称性可知:EF=2FO=4 ;
;
解法二:过点E作EH⊥AD于点H,连BF,
由折叠可知DE=BE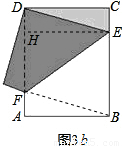
∵AF=FG,DF=AB,GD=AB
∴△ABF≌△GDF
又∵∠GDF=∠CDE,GD=CD
∴Rt△GDF≌Rt△CDE
∴DF=DE=BE
在Rt△DCE中,DC2+CE2=DE2
∵CB=25,CD=20,202+CE2=(25-CE)2
∴CE=4.5,BE=25-4.5=20.5,HF=20.5-4.5=16
在Rt△EHF中
∵EH2+HF2=FE2,202+162=FE2
∴EF=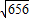 =4
=4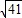 cm.
cm.
点评:本题考查图形的折叠与拼接,同时考查了三角形、四边形等几何基本知识,解题时应分别对每一个图形进行仔细分析.
解答:
 解:(1)∵由折叠可知△ABE为等腰直角三角形,
解:(1)∵由折叠可知△ABE为等腰直角三角形,∴AE=
 AB=20
AB=20 cm;
cm;(2)∵由折叠可知,AG=AB,∠GAE=∠BAE,
∵点P为AB的中点
∴AP=
 AB
AB
∴AP=
 AG
AG在Rt△APG中,得∠GAP=60°
∴∠EAB=30°
在Rt△EAB中,AE=
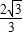 AB=
AB=
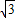 cm;
cm;(3)解法一:连接BD,交EF于点O,
由勾股定理得:BD=
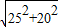 =5
=5

由折叠可知,折痕EF为BD的垂直平分线
∴OD=
 BD=
BD=
可证△DOF∽△DAB
∴
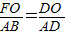
∴FO=2
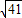
由对称性可知:EF=2FO=4
 ;
;解法二:过点E作EH⊥AD于点H,连BF,
由折叠可知DE=BE

∵AF=FG,DF=AB,GD=AB
∴△ABF≌△GDF
又∵∠GDF=∠CDE,GD=CD
∴Rt△GDF≌Rt△CDE
∴DF=DE=BE
在Rt△DCE中,DC2+CE2=DE2
∵CB=25,CD=20,202+CE2=(25-CE)2
∴CE=4.5,BE=25-4.5=20.5,HF=20.5-4.5=16
在Rt△EHF中
∵EH2+HF2=FE2,202+162=FE2
∴EF=
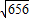 =4
=4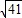 cm.
cm.点评:本题考查图形的折叠与拼接,同时考查了三角形、四边形等几何基本知识,解题时应分别对每一个图形进行仔细分析.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目