题目内容
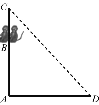
【题目】如图,在△ABC 中 AB=AC,D、E 两点分别在 AC、BC 上,BD 是∠ABC 的平分线,DE∥AB,若 BE=5cm,CE=3cm,则△CDE 的周长是( )

A. 13cmB. 11cmC. 9cmD. 8cm
【答案】A
【解析】
根据等腰三角形的性质得出∠ABC=∠C,再根据平行线的性质得出∠DEC=∠ABC=∠C,∠ABD=∠BDE,从而证出DE=DC,再根据BD是∠ABC的平分线证出∠ABD=∠DBE,∠DBE=∠BDE,最后求出BE=DE=DC,即可得出△CDE的周长.
∵AB=AC,
∴∠ABC=∠C.
∵DE∥AB,
∴∠DEC=∠ABC=∠C,∠ABD=∠BDE,
∴DE=DC,
∵BD是∠ABC的平分线,
∴∠ABD=∠DBE.
∴∠DBE=∠BDE,
∴BE=DE=DC=5cm,
∴△CDE的周长为DE+DC+EC=5+5+3=13(cm),
故选:A.

练习册系列答案
相关题目