题目内容
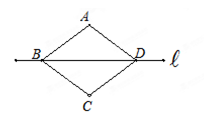
如图，直线L是四边形ABCD的对称轴，若AB=CD，有下列结论：（1）AC⊥BD；（2）AB∥CD；（3）AO=CO；（4）AB⊥BC．其中正确的结论有（ ）个．分析：根据轴对称的性质可得AB=AD，BC=CD，然后求出AB=BC=CD=AD，从而判断出四边形ABCD是菱形，再根据菱形的性质解答．
解答：解：∵直线L是四边形ABCD的对称轴，
∴AB=AD，BC=CD，
∵AB=CD，
∴AB=BC=CD=AD，
∴四边形ABCD是菱形，
∴AC⊥BD，AB∥CD，AO=CO，故（1）（2）（3）正确，
AB⊥BC只有菱形是正方形时成立，故（4）不一定正确，
综上所述，正确的结论有3个．
故选B．
∴AB=AD，BC=CD，
∵AB=CD，
∴AB=BC=CD=AD，
∴四边形ABCD是菱形，
∴AC⊥BD，AB∥CD，AO=CO，故（1）（2）（3）正确，
AB⊥BC只有菱形是正方形时成立，故（4）不一定正确，
综上所述，正确的结论有3个．
故选B．
点评：本题考查了轴对称的性质，菱形的判定与性质，熟记轴对称的性质并求出四边形ABCD是菱形是解题的关键．
练习册系列答案
53天天练系列答案
相关题目
17、如图，直线l是四边形ABCD的对称轴，若AB=CD，有下面的结论：①AB∥CD；②AC⊥BD；③AO=OC；④AB⊥BC．其中正确的结论有
30、如图，直线l是四边形ABCD的对称轴．若AD∥BC，则下列结论：①AB∥CD；②AB=BC；③AB⊥BC；④AO=OC．其中正确的是（ ）
