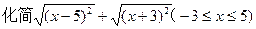题目内容
阅读材料,解答下列问题.
例:当a>0时,如a=6则|a|=|6|=6,故此时a的绝对值是它本身;
当a=0时,|a|=0,故此时a的绝对值是零;
当a<0时,如a=-6则|a|=|-6|=-(-6),故此时a的绝对值是它的相反数.
∴综合起来一个数的绝对值要分三种情况,即
|a|=
问:(1)这种分析方法涌透了
(2)请仿照例中的分类讨论的方法,分析二次根式
的各种展开的情况.
(3)猜想
与|a|的大小关系.
(4)尝试用从以上探究中得到的结论来解决下面的问题:化简
+
(-3≤x≤5).
例:当a>0时,如a=6则|a|=|6|=6,故此时a的绝对值是它本身;
当a=0时,|a|=0,故此时a的绝对值是零;
当a<0时,如a=-6则|a|=|-6|=-(-6),故此时a的绝对值是它的相反数.
∴综合起来一个数的绝对值要分三种情况,即
|a|=
|
问:(1)这种分析方法涌透了
分类讨论
分类讨论
数学思想.(2)请仿照例中的分类讨论的方法,分析二次根式
| a2 |
(3)猜想
| a2 |
(4)尝试用从以上探究中得到的结论来解决下面的问题:化简
| (x-5)2 |
| (x+3)2 |
分析:(1)根据数学上的分类讨论思想得出即可;
(2)利用利用分类讨论得出即可;
(3)利用化简结果得出即可;
(4)利用(2)中所求进而化间得出即可.
(2)利用利用分类讨论得出即可;
(3)利用化简结果得出即可;
(4)利用(2)中所求进而化间得出即可.
解答:解:(1)分类讨论;
(2)当a>时,如a=5则
=
=6,故此时
展开后是它本身,
当a=0时,
=
=0,故此时
是零,
当a<0时,如a=-6,则
=
=6,
故此时
的展开后是它的相反数,
∴综合起来一个数的绝对值要分三种情况,
=
;
(3)
=|a|;
(4)
+
(-3≤x≤5)
=|x-5|+|x+3|
=5-x+x+3
=8.
(2)当a>时,如a=5则
| 62 |
| 36 |
| a2 |
当a=0时,
| 02 |
| 0 |
| a2 |
当a<0时,如a=-6,则
| (-6)2 |
| 36 |
故此时
| a2 |
∴综合起来一个数的绝对值要分三种情况,
| a2 |
|
(3)
| a2 |
(4)
| (x-5)2 |
| (x+3)2 |
=|x-5|+|x+3|
=5-x+x+3
=8.
点评:此题主要考查了二次根式的化简求值,正确化简二次根式利用分类讨论得出是解题关键.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身 时,
时, ,故此时
,故此时 时,如
时,如 则
则 ,故此时
,故此时 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 的大小关系.
的大小关系.
 时,如
时,如 则
则 ,故此时
,故此时 的绝对值是它本身
的绝对值是它本身 时,
时, ,故此时
,故此时 时,如
时,如 则
则 ,故此时
,故此时 综合起来一个数的绝对值要分三种情况,即
综合起来一个数的绝对值要分三种情况,即
 的各种展开的情况.
的各种展开的情况. (3)猜想
(3)猜想 的大小关系.
的大小关系.