题目内容
如图,设点D、E分别为△ABC的外接圆的弧AB、弧AC的中点,弦DE交AB于点F,交AC于点G.求证:AF•AG=DF•EG.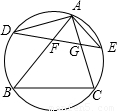
【答案】分析:根据相似三角形的判定定理AA证得△ADF∽△EAG,然后由相似三角形的对应边成比例求得 =
= ,即AF•AG=DF•EG.
,即AF•AG=DF•EG.
解答:证明:∵D、E分别是AB、AC的中点,
∴AD=BD,AE=CE,
∴∠BAD=∠E,(等弧所对的圆周角相等)
∠CAE=∠D,
∴△ADF∽△EAG
(两对应角相等,两三角形相似)
∴ =
= ,
,
∴AF•AG=DF•EG.
(说明:不填写理由共扣(1分).)
点评:本题考查了相似三角形的判定与性质、圆周角定理.在证明△ADF∽△EAG时,利用等弧所对的弦相等证明AD=BD,AE=CE是关键.
 =
= ,即AF•AG=DF•EG.
,即AF•AG=DF•EG.解答:证明:∵D、E分别是AB、AC的中点,
∴AD=BD,AE=CE,
∴∠BAD=∠E,(等弧所对的圆周角相等)
∠CAE=∠D,
∴△ADF∽△EAG
(两对应角相等,两三角形相似)
∴
 =
= ,
,∴AF•AG=DF•EG.
(说明:不填写理由共扣(1分).)
点评:本题考查了相似三角形的判定与性质、圆周角定理.在证明△ADF∽△EAG时,利用等弧所对的弦相等证明AD=BD,AE=CE是关键.

练习册系列答案
相关题目
 如图,设点D、E分别为△ABC的外接圆的弧AB、弧AC的中点,弦DE交AB于点F,交AC于点G.求证:AF•AG=DF•EG.
如图,设点D、E分别为△ABC的外接圆的弧AB、弧AC的中点,弦DE交AB于点F,交AC于点G.求证:AF•AG=DF•EG.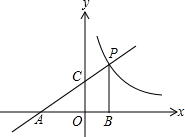 ⊥x轴,B为垂足,S△ABP=9.
⊥x轴,B为垂足,S△ABP=9.
 如图,设点D、E分别为△ABC的外接圆的弧AB、弧AC的中点,弦DE交AB于点F,交AC于点G.求证:AF•AG=DF•EG.
如图,设点D、E分别为△ABC的外接圆的弧AB、弧AC的中点,弦DE交AB于点F,交AC于点G.求证:AF•AG=DF•EG.