题目内容
如图,直线y=| 1 | 2 |
(1)求点A、C的坐标;

(2)求反比例函数解析式;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
分析:(1)要求点A、C的坐标,因为点A、C分别在x、y轴上.可以设出A(a,0),C(0,c)代入直线的解析式可知.
(2)证明△AOC∽△ABP,利用线段比求出BP,AB的值从而可求出点P的坐标即可;
(2)设R点坐标为(x,y),求出反比例函数.又因为△BRT∽△AOC,利用线段比联立方程组求出x,y的值.
(2)证明△AOC∽△ABP,利用线段比求出BP,AB的值从而可求出点P的坐标即可;
(2)设R点坐标为(x,y),求出反比例函数.又因为△BRT∽△AOC,利用线段比联立方程组求出x,y的值.
解答:解:(1)设A(a,0),C(0,c)由题意得
解得:
∴A(-4,0),C(0,2)
(2)根据已知条件可得A点坐标为(-4,0),
C点坐标为(0,2),
即AO=4,OC=2,
又∵S△ABP=9,
∴AB•BP=18,
又∵PB⊥x轴?OC∥PB,
∴△AOC∽△ABP,
∴
=
即
=
,
∴2BP=AB,
∴2BP2=18,
∴BP2=9,
∴BP=3,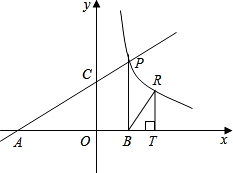
∴AB=6,
∴P点坐标为(2,3);
设反比例函数的解析式为y=
,
由题意得y=
,解得k=6
∴反比例函数的解析式为y=
;
(3)设R点的坐标为(x,y)
∵P点坐标为(2,3),
∴反比例函数解析式为y=
,
当△BTR∽△AOC时,
∴
=
,
即
=
,
则有
,
解得
,
当△BRT∽△COA时
∴
=
,
即
=
解得x1=3,x2=-1(不符合题意应舍去)
∴R的坐标为(
+1,
)或(3,2).
|
解得:
|
∴A(-4,0),C(0,2)
(2)根据已知条件可得A点坐标为(-4,0),
C点坐标为(0,2),
即AO=4,OC=2,
又∵S△ABP=9,
∴AB•BP=18,
又∵PB⊥x轴?OC∥PB,
∴△AOC∽△ABP,
∴
| AO |
| AB |
| OC |
| BP |
| 4 |
| AB |
| 2 |
| BP |
∴2BP=AB,
∴2BP2=18,
∴BP2=9,
∴BP=3,

∴AB=6,
∴P点坐标为(2,3);
设反比例函数的解析式为y=
| k |
| x |
由题意得y=
| k |
| 2 |
∴反比例函数的解析式为y=
| 6 |
| x |
(3)设R点的坐标为(x,y)
∵P点坐标为(2,3),
∴反比例函数解析式为y=
| 6 |
| x |
当△BTR∽△AOC时,
∴
| AO |
| OC |
| BT |
| RT |
即
| 4 |
| 2 |
| x-2 |
| y |
则有
|
解得
|
当△BRT∽△COA时
∴
| AO |
| OC |
| RT |
| BT |
即
| 4 |
| 2 |
| y |
| x-2 |
解得x1=3,x2=-1(不符合题意应舍去)
∴R的坐标为(
| 13 |
| ||
| 2 |
点评:本题考查的是一次函数和反比例函数的综合运用以及相似三角形的判定,待定系数法求函数的解析式.难度中上.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
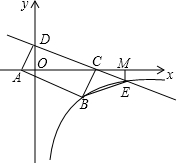 如图,直线y=-
如图,直线y=-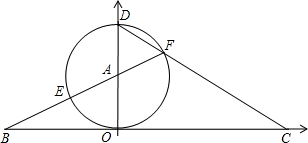 D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B.
D为直径作⊙A交CD于F,FA的延长线交⊙A于E,交x轴于B.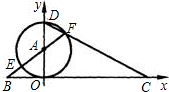 如图,直线y=-
如图,直线y=-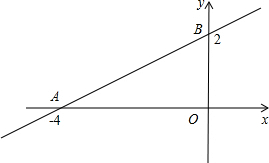 如图,直线y=
如图,直线y= (2013•蒙山县一模)如图,直线
(2013•蒙山县一模)如图,直线