题目内容
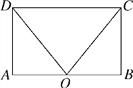
【题目】如图，在矩形ABCD中，点O在边AB上，∠AOC＝∠BOD.求证：AO＝OB.
【答案】证明见解析
【解析】【试题分析】根据矩形的性质，得：∠A＝∠B＝90°，AD＝BC.
∵∠AOC＝∠BOD，根据等式的性质得：∠AOC－∠DOC＝∠BOD－∠DOC，即∠AOD＝∠BOC. 在△AOD和△BOC中，∠A＝∠B，∠AOD＝∠BOC，AD＝BC，根据AAS判定，得：△AOD≌△BOC，根据全等三角形对应边相等，得：AO＝OB.
【试题解析】
∵四边形ABCD是矩形，∴∠A＝∠B＝90°，AD＝BC.
∵∠AOC＝∠BOD，∴∠AOC－∠DOC＝∠BOD－∠DOC，即∠AOD＝∠BOC.
在△AOD和△BOC中，∠A＝∠B，∠AOD＝∠BOC，AD＝BC，
∴△AOD≌△BOC，∴AO＝OB.
练习册系列答案
相关题目
【题目】某班10名学生的校服尺寸与对应人数如表所示：
尺寸（cm） | 160 | 165 | 170 | 175 | 180 |
学生人数（人） | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为（ ）
A.165cm，165cm
B.165cm，170cm
C.170cm，165cm
D.170cm，170cm
【题目】下表中有两种移动电话计费方式．
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟
是正整数
．
当
时，按方式一计费为______元；按方式二计费为______元；
当
时，是否存在某一时间t，使两种计费方式相等，若存在，请求出对应t的值，若不存在，请说明理由；
当
时，请直接写出省钱的计费方式？
