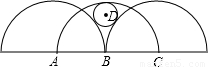
题目内容
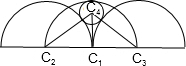 三个半圆的半径均为R,圆心C1,C2,C3在同一直线上,且每一圆心都在另一半圆的圆周上,⊙C4与这三个半圆都相切,设⊙C4的半径为r,则R:r等于(C )
三个半圆的半径均为R,圆心C1,C2,C3在同一直线上,且每一圆心都在另一半圆的圆周上,⊙C4与这三个半圆都相切,设⊙C4的半径为r,则R:r等于(C )
- A.15:4
- B.11:3
- C.4:1
- D.3:1
C
分析:要求R:r,由题中⊙C4与这三个半圆都相切知C2C4=C3C4=R+r,C1C4=R-r,进而得C1C4⊥C1C3
所以在△C1C3C4中由勾股定理得R=4r,所以R:r=4:1
解答:设小圆半径为r,
∵⊙C4与这三个半圆都相切,
∴C2C4=C3C4=R+r,C1C4=R-r,
所以△C2C3C4是等腰三角形,
又∵C2C1=C1C3
∴C1C4⊥C1C3
∴在△C1C3C4中
(R-r)2+R2=(R+r)2
∴R=4r,
∴R:r=4:1,
故选C
点评:这道题考查了相切圆的性质以及勾股定理,同学们应熟练掌握.
分析:要求R:r,由题中⊙C4与这三个半圆都相切知C2C4=C3C4=R+r,C1C4=R-r,进而得C1C4⊥C1C3
所以在△C1C3C4中由勾股定理得R=4r,所以R:r=4:1
解答:设小圆半径为r,
∵⊙C4与这三个半圆都相切,
∴C2C4=C3C4=R+r,C1C4=R-r,
所以△C2C3C4是等腰三角形,
又∵C2C1=C1C3
∴C1C4⊥C1C3
∴在△C1C3C4中
(R-r)2+R2=(R+r)2
∴R=4r,
∴R:r=4:1,
故选C
点评:这道题考查了相切圆的性质以及勾股定理,同学们应熟练掌握.

练习册系列答案
相关题目
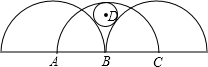 如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为( )
如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为( )| A、15:4 | B、11:3 | C、4:1 | D、3:1 |
 3、三个半圆的半径均为R,圆心C1,C2,C3在同一直线上,且每一圆心都在另一半圆的圆周上,⊙C4与这三个半圆都相切,设⊙C4的半径为r,则R:r等于(C )
3、三个半圆的半径均为R,圆心C1,C2,C3在同一直线上,且每一圆心都在另一半圆的圆周上,⊙C4与这三个半圆都相切,设⊙C4的半径为r,则R:r等于(C ) 如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为
如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为