题目内容
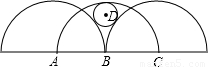
 如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为
如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为
- A.15:4
- B.11:3
- C.4:1
- D.3:1
C
分析:要求R:r,应该构建三角形,根据三角形边角关系确定其比值,所以连接BD,CD,△BCD是直角三角形,三边分别用R,r表示,然后由勾股定理就可确定R:r值.
解答: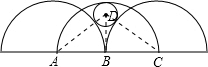 解:如图,连接BD,CD,AD,
解:如图,连接BD,CD,AD,
则BD=R-r,CD=R+r,BC=R,
∵AD=CD,AB=BC,
∴BD⊥AC
根据勾股定理BD2+BC2=CD2.
即R2+r2-2Rr+R2=R2+r2+2Rr,
则R2=4Rr,
∴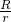 =
=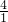 .
.
点评:这道题考查了相切圆的性质,以及勾股定理的应用,同学们应熟练掌握.
分析:要求R:r,应该构建三角形,根据三角形边角关系确定其比值,所以连接BD,CD,△BCD是直角三角形,三边分别用R,r表示,然后由勾股定理就可确定R:r值.
解答:
 解:如图,连接BD,CD,AD,
解:如图,连接BD,CD,AD,则BD=R-r,CD=R+r,BC=R,
∵AD=CD,AB=BC,
∴BD⊥AC
根据勾股定理BD2+BC2=CD2.
即R2+r2-2Rr+R2=R2+r2+2Rr,
则R2=4Rr,
∴
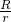 =
=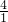 .
.点评:这道题考查了相切圆的性质,以及勾股定理的应用,同学们应熟练掌握.

练习册系列答案
相关题目
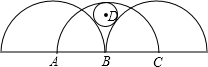 如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为( )
如图三个半圆的半径均为R,它们的圆心A、B、C半圆均相切,设⊙D的半径为r,则R:r的值为( )| A、15:4 | B、11:3 | C、4:1 | D、3:1 |
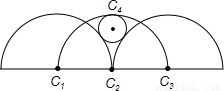
 17、如图所示,三个半圆C1、C2、C3的半径均为R,圆心共线且都在某个半圆的圆周上,圆C4与上述三个圆都相切,其半径为r,则R:r为
17、如图所示,三个半圆C1、C2、C3的半径均为R,圆心共线且都在某个半圆的圆周上,圆C4与上述三个圆都相切,其半径为r,则R:r为