题目内容
已知（m，n）是抛物线y=ax2上的点，求证：点（-m，n）也在抛物线y=ax2上．
证明：∵抛物线y=ax2的对称轴是y轴，而点（m，n）与点（-m，n）也关于y轴对称，
∴当点（m，n）在抛物线y=ax2上时，点（-m，n）也在抛物线y=ax2上．
分析：抛物线y=ax2关于y轴对称，点（m，n）与点（-m，n）也关于y轴对称，根据对称性可证结论．
点评：本题考查了抛物线y=ax2的对称性，在解抛物线问题时，需要熟练运用．
∴当点（m，n）在抛物线y=ax2上时，点（-m，n）也在抛物线y=ax2上．
分析：抛物线y=ax2关于y轴对称，点（m，n）与点（-m，n）也关于y轴对称，根据对称性可证结论．
点评：本题考查了抛物线y=ax2的对称性，在解抛物线问题时，需要熟练运用．
练习册系列答案
相关题目
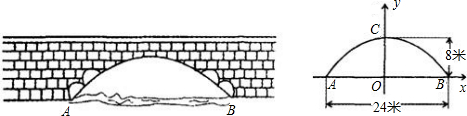
如图，某隧道口的横截面是抛物线形，已知路宽AB为6米，最高点离地面的距离OC为5米．以最高点O为坐标原点，抛物线的对称轴为y轴，1米为数轴的单位长度，建立平面直角坐标系，
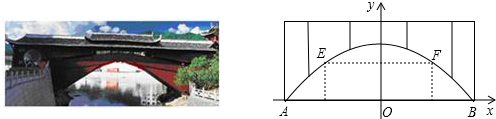
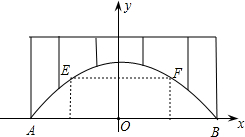廊桥是我国古老的文化遗产．如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为y=-
如图，某隧道口的横截面是抛物线形，已知路宽AB为6米，最高点离地面的距离OC为5米．以最高点O为坐标原点，抛物线的对称轴为y轴，1米为数轴的单位长度，建立平面直角坐标系．求：