题目内容
 已知直线y=
已知直线y=| 1 |
| 2 |
| 1 |
| 2 |
分析:在直线y=
x+1上取两点:(-2,0),(0,1),根据两点确定一条直线,把直线绕点A(1,0)顺时针旋转90°的问题,转化为两点(-2,0),(0,1)绕点A(1,0)顺时针旋转90°的问题,再用待定系数法求旋转后的直线解析式.
| 1 |
| 2 |
解答: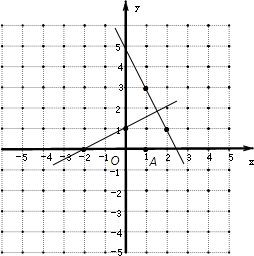 解:∵直线y=
解:∵直线y=
x+1与坐标轴交于(-2,0),(0,1)两点,
∴(-2,0),(0,1)两点绕点A(1,0)顺时针旋转90°后的坐标分别为(1,3),(2,1),
设过(1,3),(2,1)两点的直线解析式为y=kx+b,
则
,
解得:
∴旋转后的直线解析式为y=-2x+5.
 解:∵直线y=
解:∵直线y=| 1 |
| 2 |
∴(-2,0),(0,1)两点绕点A(1,0)顺时针旋转90°后的坐标分别为(1,3),(2,1),
设过(1,3),(2,1)两点的直线解析式为y=kx+b,
则
|
解得:
|
∴旋转后的直线解析式为y=-2x+5.
点评:本题考查了转化的思想,即将直线的旋转问题转化为点的旋转问题来解决.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
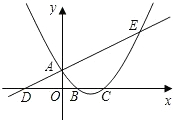 E两点,与x轴交于B、C两点,且B点坐标为(1,0).
E两点,与x轴交于B、C两点,且B点坐标为(1,0).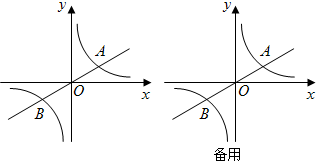
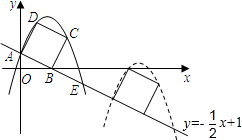 (2013•梧州模拟)如图,已知直线y=
(2013•梧州模拟)如图,已知直线y=