题目内容
有一张矩形纸片ABCD,E、F分别是BC、AD上的点(但不与顶点重合),若EF将矩形ABCD分成面积相等的两部分,设AB=m,AD=n,BE=x.(1)求证:AF=EC;
(2)用剪刀将该纸片沿直线EF剪开后,再将梯形纸片ABEF沿AB对称翻折,平移拼接在梯形ECDF的下方,使一底边重合,一腰落在DC的延长线上,拼
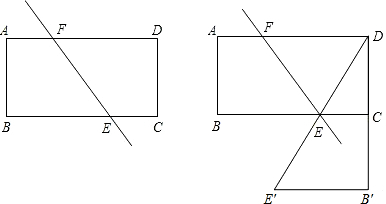 接后,下方梯形记作EE′B′C.当x:n为何值时,直线E′E经过原矩形的顶点D.
接后,下方梯形记作EE′B′C.当x:n为何值时,直线E′E经过原矩形的顶点D.
分析:(1)根据题知,EF将矩形分割为两个面积相等的梯形,而且两个梯形腰相等,利用面积相等易证;
(2)可先假设直线E′E经过原矩形的顶点D,再根据梯形纸片沿着AB翻折后可知DC=BC=m,然后利用中位线定理可知DE=E′E 2EC=E′B′然后分别代入可求:
(2)可先假设直线E′E经过原矩形的顶点D,再根据梯形纸片沿着AB翻折后可知DC=BC=m,然后利用中位线定理可知DE=E′E 2EC=E′B′然后分别代入可求:
解答:(1)证明:∵EF将矩形ABCD分成面积相等的两部分,
∴
(x+AF)•m=
(n-x+n-AF)•m,(2分)
∴2AF=2n-2x,
∴AF=n-x,(3分)
又∵EC=BC-BE=n-x,
∴AF=EC;(4分)
(2)解:当直线E′E经过原矩形的顶点D时,如图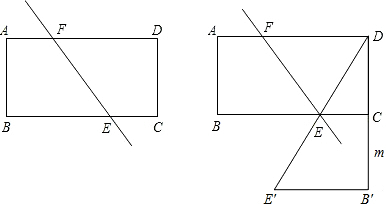
∵DC=B′C=m,EC∥E′B′,
∴DE=E′E.
∴2EC=E′B′.
即2(n-x)=x,
∴2n=3x.(7分)
∴x:n=2:3.(9分)
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴2AF=2n-2x,
∴AF=n-x,(3分)
又∵EC=BC-BE=n-x,
∴AF=EC;(4分)
(2)解:当直线E′E经过原矩形的顶点D时,如图

∵DC=B′C=m,EC∥E′B′,
∴DE=E′E.
∴2EC=E′B′.
即2(n-x)=x,
∴2n=3x.(7分)
∴x:n=2:3.(9分)
点评:本题涉及矩形的性质,解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.而不是思维定势只利用传统思维的直接求证方式.

练习册系列答案
相关题目
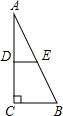 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一




 = ;
= ; 




 = ;
= ; 