Question

某商店经销甲、乙两种商品. 现有如下信息:

请根据以上信息，解答下列问题：

（1）甲、乙两种商品的进货单价各多少元?

（2）该商店平均每天卖出甲商品600件和乙商品400件．经调查发现，甲、乙两种商品零售单价分别每降0.1元，这两种商品每天可各多销售100件．为了使每天获取更大的利润，商店决定把甲、乙两种商品的零售单价都下降m元. 在不考虑其他因素的条件下，当m定为多少时，才能使商店每天销售甲、乙两种商品获取的利润最大？每天的最大利润是多少?

 

Answer 1

【答案】

（1）甲商品的进货单价是2元，乙商品的进货单价是3元

（2）当m定为0.5时，才能使商店每天销售甲、乙两种商品获取的利润最大，每天的最大利润是1900元.

【解析】

试题分析：（1）设甲商品的进货单价是x元，乙商品的进货单价是y元．

根据题意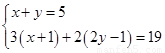，得   解得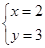 

答：甲商品的进货单价是2元，乙商品的进货单价是3元．      

（2）设商店每天销售甲、乙两种商品获取的利润为s元，则

s=(1-m)(600+100×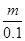)+(5-3-m)(400+100×)           

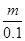即 s=-2000m²+2000m+1400  =-2000(m-0.5)²+1900.

∴当m=0.5时，s有最大值，最大值为1900.             

答：当m定为0.5时，才能使商店每天销售甲、乙两种商品获取的利润最大，每天的最大利润是1900元.                

考点：二元一次方程、求函数的最大值

点评：本题考查二元一次方程、求函数的最大值，考生会解二元一次方程组，会用配方法求二次函数的最值