题目内容
 (2012•东莞)已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,BO=DO.
(2012•东莞)已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,BO=DO.求证:四边形ABCD是平行四边形.
分析:先根据AB∥CD可知∠ABO=∠CDO,再由BO=DO,∠AOB=∠DOC即可得出△ABO≌△CDO,故可得出AB=CD,进而可得出结论.
解答:证明:∵AB∥CD,
∴∠ABO=∠CDO,
在△ABO与△CDO中,
∵
,
∴△ABO≌△CDO,
∴AB=CD,
∴四边形ABCD是平行四边形.
∴∠ABO=∠CDO,
在△ABO与△CDO中,
∵
|
∴△ABO≌△CDO,
∴AB=CD,
∴四边形ABCD是平行四边形.
点评:本题考查的是平行四边形的判定、全等三角形的判定与性质,熟知平行四边形的判定定理是解答此题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
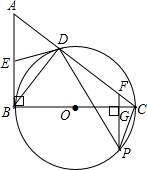 (2012•东莞模拟)如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F
(2012•东莞模拟)如图,已知AB是⊙O的切线,BC为⊙O的直径,AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F (2012•东莞模拟)如图,已知△ABC中,AB=AC,
(2012•东莞模拟)如图,已知△ABC中,AB=AC,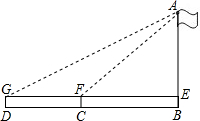 (2012•东莞模拟)如图,九年级某班同学要测量校园内旗杆的高度,在地面的C点处用测角器测得旗杆顶A点的仰角∠AFE=45°,再沿直线CB后退12m到D点,在D点又用测角器测得旗杆顶A点的仰角∠AGE=30°;已知测角器的高度为1.7m,求旗杆AB的高度(结果保留一位小数).
(2012•东莞模拟)如图,九年级某班同学要测量校园内旗杆的高度,在地面的C点处用测角器测得旗杆顶A点的仰角∠AFE=45°,再沿直线CB后退12m到D点,在D点又用测角器测得旗杆顶A点的仰角∠AGE=30°;已知测角器的高度为1.7m,求旗杆AB的高度(结果保留一位小数).