题目内容
已知反比例函数y=
图象在一、三象限内,则一次函数y=kx-4的图象经过的象限是( )
| -k |
| x |
| A、第一、二、三象限 |
| B、第一、二、四象限 |
| C、第二、三、四象限 |
| D、第一、三、四象限 |
练习册系列答案
相关题目
下列等式成立的是( )
| A、(-2)-2=-4 | ||
| B、(-2)-2=4 | ||
C、(-2)2=-
| ||
D、(-2)2=
|
求一元二次方程x2+3x-1=0的解,除了课本的方法外,我们也可以采用图象的方法:在平面直角坐标系中,画出直线y=x+3和双曲线y=
的图象,则两图象交点的横坐标即该方程的解.类似地,我们可以判断方程x3-x-1=0的解的个数有( )
| 1 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
若函数y=
的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
| 1-m |
| x |
| A、m>1 | B、m>0 |
| C、m<1 | D、m<0 |
反比例函数y=
的图象在第一、三象限内,则m的取值范围是( )
| m-2 |
| x |
| A、m<0 | B、m<2 |
| C、m>0 | D、m>2 |
 如图,过点O作直线与双曲线y=
如图,过点O作直线与双曲线y=| k |
| x |
| A、S1=S2 |
| B、2S1=S2 |
| C、3S1=S2 |
| D、4S1=S2 |
 如图,反比例函数与正比例函数的图象交于A、B两点,过点A作AC⊥y轴于点C,连接BC.若△ABC的面积是4,则这个反比例函数的表达式是( )
如图,反比例函数与正比例函数的图象交于A、B两点,过点A作AC⊥y轴于点C,连接BC.若△ABC的面积是4,则这个反比例函数的表达式是( )A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
 如图,在平面直角坐标系中,反比例函数y1=
如图,在平面直角坐标系中,反比例函数y1=| 2 |
| x |
| A、1<x<3 |
| B、x<0或1<x<3 |
| C、0<x<1 |
| D、x>3或0<x<1 |

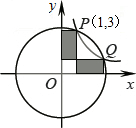 如图,双曲线y=
如图,双曲线y=