题目内容
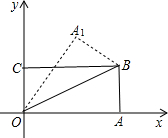 如图,OA=
如图,OA=| 3 |
分析:由已知可得∠AOB=30°,翻折后找到相等的角及相等的边,在直角三角形中,利用勾股定理可求得答案.
解答:解:过A1作A1D⊥OA,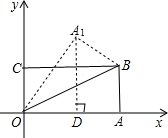
在Rt△OAB中,OB=
=2,AB=1,
∴AB=
OB,
∵△AOB是直角三角形,
∴∠AOB=30°,
OB为折痕,
∴∠A1OB=∠AOB=30°,OA1=OA=
,
Rt△OA1D中,∠OA1D=30°,
∴OD=
×
=
,
A1D=
×
=
,
∴点A1的坐标(
,
).
故答案为:(
,
).

在Rt△OAB中,OB=
(
|
∴AB=
| 1 |
| 2 |
∵△AOB是直角三角形,
∴∠AOB=30°,
OB为折痕,
∴∠A1OB=∠AOB=30°,OA1=OA=
| 3 |
Rt△OA1D中,∠OA1D=30°,
∴OD=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
A1D=
| ||
| 2 |
| 3 |
| 3 |
| 2 |
∴点A1的坐标(
| ||
| 2 |
| 3 |
| 2 |
故答案为:(
| ||
| 2 |
| 3 |
| 2 |
点评:本题考查了含30°的直角三角形的性质、勾股定理及翻折问题;利用翻折找准相等的角、相等的边是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
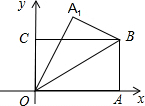 如图,OA=2,AB=1的矩形OABC在直角坐标系中,将矩形OABC沿OB对折,点A落在点A1,则点A1的坐标是
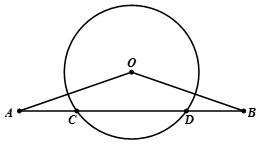
如图,OA=2,AB=1的矩形OABC在直角坐标系中,将矩形OABC沿OB对折,点A落在点A1,则点A1的坐标是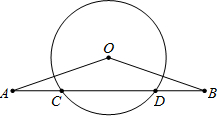 如图,OA=OB,AB交⊙O于点C、D,AC与BD是否相等?为什么?
如图,OA=OB,AB交⊙O于点C、D,AC与BD是否相等?为什么?