题目内容
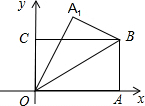如图，OA=2，AB=1的矩形OABC在直角坐标系中，将矩形OABC沿OB对折，点A落在点A1，则点A1的坐标是分析：过点A1作A1F⊥x轴于F，交BC于E，设OA1与BC交于D，易知OD=BD，设BD=x，则OD=x，CD=2-x，在直角△OCD中，由勾股定理知x=
，则A1D=
，又△OCD∽△A1ED，得A1E=
，则A1F=
，由勾股定理求得OF=
．
| 5 |
| 4 |
| 3 |
| 4 |
| 3 |
| 5 |
| 8 |
| 5 |
| 6 |
| 5 |
解答：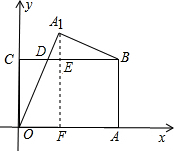
解：过点A1作A1F⊥x轴于F，交BC于E，设OA1与BC交于D，
∵∠BOA=∠BOD，∠CBO=∠BOA，
∴∠DOB=∠DBO，
∴OD=BD，
设BD=x，则OD=x，CD=2-x，
在直角△OCD中，由勾股定理知：OD2=CD2+OC2，
即：x2=（2-x）2+12，
解得：x=
，
则A1D=A1O-OD=
，
∵∠A1ED=∠OCD=90°，∠A1DE=∠CDO，
∴△OCD∽△A1ED，
∴OD：A1D=OC：A1E，
∴A1E=
，则A1F=A1E+EF=
，
∴由勾股定理得：OA12=A1F2+OF2，
∴OF=
．
∴点A1的坐标是：（
，
）．
故本题答案为：（
，
）．
解：过点A1作A1F⊥x轴于F，交BC于E，设OA1与BC交于D，∵∠BOA=∠BOD，∠CBO=∠BOA，
∴∠DOB=∠DBO，
∴OD=BD，
设BD=x，则OD=x，CD=2-x，
在直角△OCD中，由勾股定理知：OD2=CD2+OC2，
即：x2=（2-x）2+12，
解得：x=
| 5 |
| 4 |
则A1D=A1O-OD=
| 3 |
| 4 |
∵∠A1ED=∠OCD=90°，∠A1DE=∠CDO，
∴△OCD∽△A1ED，
∴OD：A1D=OC：A1E，
∴A1E=
| 3 |
| 5 |
| 8 |
| 5 |
∴由勾股定理得：OA12=A1F2+OF2，
∴OF=
| 6 |
| 5 |
∴点A1的坐标是：（
| 6 |
| 5 |
| 8 |
| 5 |
故本题答案为：（
| 6 |
| 5 |
| 8 |
| 5 |
点评：解此类题目要利用图形对折后全等的性质，运用勾股定理时要把已知条件与未知量集中在同一个三角形中．
练习册系列答案
阅读快车系列答案
相关题目
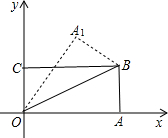如图，OA=
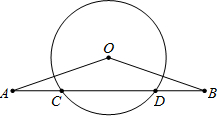如图，OA=OB，AB交⊙O于点C、D，AC与BD是否相等？为什么？
