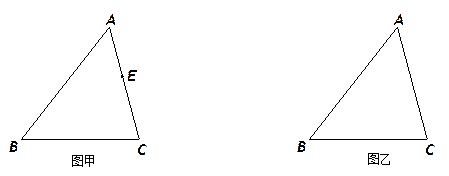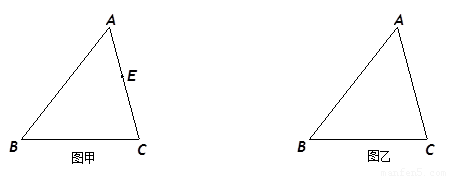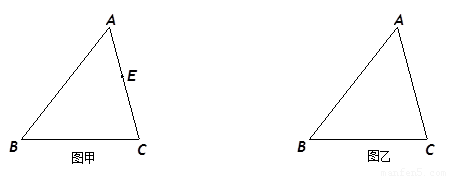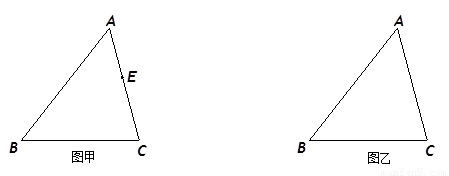题目内容
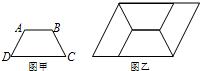14、如图甲，四边形ABCD是等腰梯形，AB∥CD，由4个这样的等腰梯形可以拼出图乙所示的平行四边形，则下列结论成立的是（ ）①∠C=60°；②AD=BC；③DC=3AB；④AB=AD．
分析：直接由等腰梯形的性质得出AD=BC，观察图乙，可以直接看出等腰梯形ABCD上底和腰相等，再由平行四边形的同旁内角互补和等腰梯形的两个底角相等可以得出∠C=60°．
解答：解：①由图乙拼出的平行四边形可以得到同旁内角互补，而且三个角都相等，所以∠C=60°；
②由梯形ABCD是等腰梯形，所以AD=BC；
③把图乙中间的底延长，可以得出DC=2AB；
④由图乙，可以直接看出等腰梯形ABCD上底和腰相等，即AB=AD．故选D．
②由梯形ABCD是等腰梯形，所以AD=BC；
③把图乙中间的底延长，可以得出DC=2AB；
④由图乙，可以直接看出等腰梯形ABCD上底和腰相等，即AB=AD．故选D．
点评：由等腰梯形的性质及平行四边形的性质，再结合图形问题自然可以解决．
练习册系列答案
相关题目
