Question

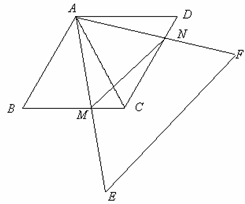
如图，四边形ABCD中，∠BAD＝∠ACB＝90°，AB＝AD，AC＝4BC，
CD＝5，则四边形ABCD的面积为______________

Answer 1

10

作AE⊥AC，DE⊥AE，两线交于E点，作DF⊥AC垂足为F点，求出∠BAC=∠DAE，根据AAS证△ABC≌△ADE，推出BC=DE，AC=AE，设BC=a，则DE=a，DF=AE=AC=4BC=4a，求出CF=3a，
在Rt△CDF中，由勾股定理得出（3a）²+（4a）²=5²，求出a=1，根据S_{四边形ABCD}=S_梯形ACDE求出梯形ACDE的面积即可．
解：作AE⊥AC，DE⊥AE，两线交于E点，作DF⊥AC垂足为F点，

∵∠BAD=∠CAE=90°，
即∠BAC+∠CAD=∠CAD+∠DAE，
∴∠BAC=∠DAE，
在△ABC和△ADE中
∵，
∴△ABC≌△ADE（AAS），
∴BC=DE，AC=AE，
设BC=a，则DE=a，DF=AE=AC=4BC=4a，
CF=AC-AF=AC-DE=3a，
在Rt△CDF中，由勾股定理得：CF²+DF²=CD²，
即（3a）²+（4a）²=5²，
解得：a=1，
∴S_{四边形ABCD}=S_梯形ACDE=×（DE+AC）×DF
=×（a+4a）×4a
=10a²
=10．
故答案为：10．