题目内容
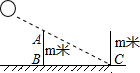冬至是一年中太阳相对于地球位置最低的时刻，只要此时能采到阳光，一年四季就均能受到阳光照射．此时竖一根a米长的竹竿，其影长为b米，某单位计划想建m米高的南北两幢宿舍楼（如图所示）．试问两幢楼相距多少米时，后楼的采光一年四季不受影响（用m，a，b表示）．
解：根据题意可得：
=
，
∵AB=m，
∴BC=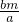
，
∴两幢楼相距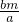米时，后楼的采光一年四季不受影响．
分析：运用同一时刻物体与影长成比例，得出=，进而求出即可．
点评：此题主要考查了相似三角形的应用，根据已知得出同一时刻物体的影长与物体高度比值相等是解决问题的关键．
=，∵AB=m，
∴BC=
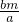，∴两幢楼相距
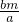米时，后楼的采光一年四季不受影响．分析：运用同一时刻物体与影长成比例，得出
=，进而求出即可．点评：此题主要考查了相似三角形的应用，根据已知得出同一时刻物体的影长与物体高度比值相等是解决问题的关键．
练习册系列答案
相关题目
居民楼的采光是人们购买楼房时关心的一个重要问题，冬至是一年中太阳相对地球北半球位置最低的时刻，只要此时楼房的最低层能采到阳光，一年四季整座楼均能受到阳光的照射，某地区冬至时阳光与地面所成的角约为30°，如图所示．现有A、B、C、D四种设计方案提供的居民甲楼的高H（米）与两楼间距L（米）的数据，如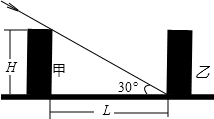
下表所示．仅就图中居民楼乙的采光问题，你认为哪种方案设计较为合理，并说明理由．（参考数据
=1.732）
下表所示．仅就图中居民楼乙的采光问题，你认为哪种方案设计较为合理，并说明理由．（参考数据| 3 |
| A | B | C | D | |
| H（米） | 12 | 15 | 16 | 18 |
| L（米） | 18 | 25 | 28 | 30 |
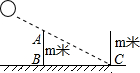冬至是一年中太阳相对于地球位置最低的时刻，只要此时能采到阳光，一年四季就均能受到阳光照射．此时竖一根a米长的竹竿，其影长为b米，某单位计划想建m米高的南北两幢宿舍楼（如图所示）．试问两幢楼相距多少米时，后楼的采光一年四季不受影响（用m，a，b表示）．
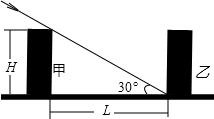下表所示．仅就图中居民楼乙的采光问题，你认为哪种方案设计较为合理，并说明理由．（参考数据
=1.732）