题目内容
已知O是?ABCD两对角线AC，BD的交点，AC=12cm，BD=16cm，AD=10cm，则?ABCD为________．
（填写：矩形、菱形、正方形之一）
菱形
分析：根据平行四边形的性质求出OA、OD的长，计算出AO和OD的平方和，根据勾股定理的逆定理求出∠AOD=90°，根据菱形的判定证出即可．
解答：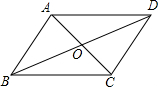
解：∵平行四边形ABCD，
∴OA=OC=
AC=6，OB=0D=BD=8，
∵AD=10，
∴OA2+OD2=100，
AD2=100，
∴OA2+OD2=AD2，
∴∠AOD=90°，
即AC⊥BD，
∵四边形ABCD是平行四边形，
∴平行四边形ABCD是菱形．
故答案为：菱形．
点评：本题主要考查对平行四边形的性质，菱形的判定，勾股定理的逆定理等知识点的理解和掌握，能证出∠AOD=90°是解此题的关键．
分析：根据平行四边形的性质求出OA、OD的长，计算出AO和OD的平方和，根据勾股定理的逆定理求出∠AOD=90°，根据菱形的判定证出即可．
解答：
解：∵平行四边形ABCD，∴OA=OC=
AC=6，OB=0D=BD=8，∵AD=10，
∴OA2+OD2=100，
AD2=100，
∴OA2+OD2=AD2，
∴∠AOD=90°，
即AC⊥BD，
∵四边形ABCD是平行四边形，
∴平行四边形ABCD是菱形．
故答案为：菱形．
点评：本题主要考查对平行四边形的性质，菱形的判定，勾股定理的逆定理等知识点的理解和掌握，能证出∠AOD=90°是解此题的关键．
练习册系列答案
相关题目
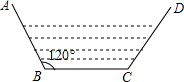某村计划修建一条水渠，其横断面是等腰梯形，底角B为120°，如图所示，已知等腰梯形ABCD两腰与底边BC的和为4m，则梯形的最大面积为