题目内容
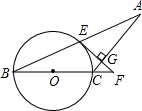 已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G交BC的延长线于F.
已知,如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G交BC的延长线于F.(1)求证:AE=BE;
(2)求证:FE是⊙O的切线;
(3)若BC=6,FE=4,求FC和AG的长.
分析:(1)连接CE和OE,因为BC是直径,所以∠BEC=90°,即CE⊥BE;再根据等腰三角形三线合一定理,可以知道CE也是AB的中线,即AE=BE.
(2)根据已知得OE是△ABC的中线,从而得到∠OEC=∠ECG,进而可得到∠OEF=90°,那么就证出EF是切线.
(3)直接利用切割线定理求出CF的长,利用OE∥AC,可以得到比例线段,求出CG的长,那么AG=AC-CG,AG就可求得.
(2)根据已知得OE是△ABC的中线,从而得到∠OEC=∠ECG,进而可得到∠OEF=90°,那么就证出EF是切线.
(3)直接利用切割线定理求出CF的长,利用OE∥AC,可以得到比例线段,求出CG的长,那么AG=AC-CG,AG就可求得.
解答: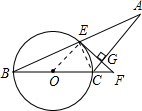 (1)证明:连接CE和OE;
(1)证明:连接CE和OE;
∵BC是直径,
∴∠BEC=90°,
∴CE⊥AB;
又∵AC=BC,
∴BE=AE.
(2)证明:∵BE=AE,OB=OC,
∴OE是△ABC的中位线,
∴OE∥AC,AC=2OE=6.
∴∠OEC=∠ACE.
又∵EG⊥AC,
∴∠CEG+∠ACE=90°,
∴∠CEG+∠OEC=90°,
∴∠OEF=90°.
∴EF是⊙O的切线.
(3)解:∵EF是⊙O的切线,
∴EF2=CF•BF.
设CF=x,则有x(x+6)=16,
解得,x1=2,x2=-8(不合题意,舍去)那么CF=2;
∵OE∥AC,
∴
=
,
∴
=
,
∴CG=
.
∴AG=AC-CG=6-
=
.
 (1)证明:连接CE和OE;
(1)证明:连接CE和OE;∵BC是直径,
∴∠BEC=90°,
∴CE⊥AB;
又∵AC=BC,
∴BE=AE.
(2)证明:∵BE=AE,OB=OC,
∴OE是△ABC的中位线,
∴OE∥AC,AC=2OE=6.
∴∠OEC=∠ACE.
又∵EG⊥AC,
∴∠CEG+∠ACE=90°,
∴∠CEG+∠OEC=90°,
∴∠OEF=90°.
∴EF是⊙O的切线.
(3)解:∵EF是⊙O的切线,
∴EF2=CF•BF.
设CF=x,则有x(x+6)=16,
解得,x1=2,x2=-8(不合题意,舍去)那么CF=2;
∵OE∥AC,
∴
| CG |
| OE |
| CF |
| OF |
∴
| CG |
| 3 |
| 2 |
| 5 |
∴CG=
| 6 |
| 5 |
∴AG=AC-CG=6-
| 6 |
| 5 |
| 24 |
| 5 |
点评:本题利用了等腰三角形三线合一定理,三角形中位线的判定,切割线定理,以及勾股定理,还有平行线分线段成比例定理,切线的判定等知识.

练习册系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.