题目内容
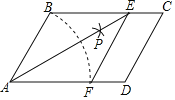
【题目】如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,以大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
求证:四边形ABEF是菱形.
【答案】见解析
【解析】分析:先证明△AEB≌△AEF,推出∠EAB=∠EAF,由AD∥BC,推出∠EAF=∠AEB=∠EAB,得到BE=AB=AF,由此即可证明.
详解:证明:连接BP、FP由作图知:AB=AF,BP=FP
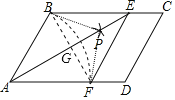
在△APB和△APF中,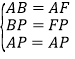
∴△APB≌△APF,∴∠EAB=∠EAF,
∵AD∥BC,
∴∠EAF=∠AEB=∠EAB,∴BE=AB=AF.
∵AF∥BE,
∴四边形ABEF是平行四边形,∵AB=BE,
四边形ABEF是菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】两枚正四面体骰子的各面上分别标有数字1,2,3,4,现在同时投掷这两枚骰子,并分别记录着地的面所得的点数为a、b.
(1)假设两枚正四面体都是质地均匀,各面着地的可能性相同,请你在下面表格内列举出所有情形(例如(1,2),表示a=1,b=2),并求出两次着地的面点数相同的概率.
b | 1 | 2 | 3 | 4 |
1 | (1,2) | |||
2 | ||||
3 | ||||
4 |
(2)为了验证试验用的正四面体质地是否均匀,小明和他的同学取一枚正四面体进行投掷试验.试验中标号为1的面着地的数据如下:
试验总次数 | 50 | 100 | 150 | 200 | 250 | 500 |
“标号1”的面着地的次数 | 15 | 26 | 34 | 48 | 63 | 125 |
“标号1”的面着地的频率 | 0.3 | 0.26 | 0.23 | 0.24 |
请完成表格(数字精确到0.01),并根据表格中的数据估计“标号1的面着地”的概率是






