题目内容
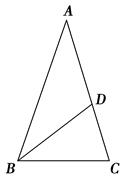
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2,则AD的长是( )

A.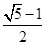 | B.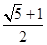 |
C.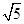 -1 -1 | D.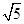 +1 +1 |
C
∵∠A=∠DBC=36°,∠C为公共角,
∴△ABC∽△BDC,且AD=BD=BC.
设BD=x,则BC=x,CD=2-x.
由于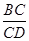 =
=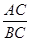 ,∴
,∴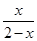 =
=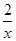 ,
,
整理得:x2+2x-4=0,解得:x=-1±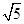 ,
,
∵x为正数,∴x=-1+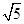 .故选C.
.故选C.
∴△ABC∽△BDC,且AD=BD=BC.
设BD=x,则BC=x,CD=2-x.
由于
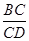 =
=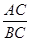 ,∴
,∴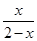 =
=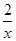 ,
,整理得:x2+2x-4=0,解得:x=-1±
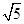 ,
,∵x为正数,∴x=-1+
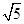 .故选C.
.故选C.
练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目

 =
= .
.
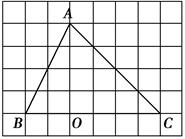
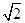 ,点A的坐标为(1,0),则E点的坐标为( )
,点A的坐标为(1,0),则E点的坐标为( )

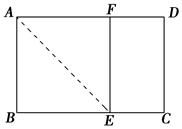
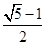
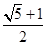
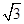
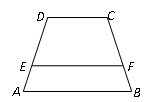
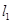 、
、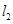 于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC= .
于点A、B、C和点D、E、F,如果DE:EF=3:5,AC=24,则BC= .