题目内容
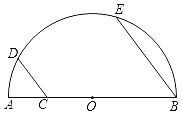
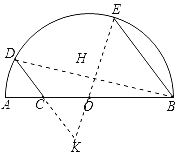
【题目】如图:AB为半圆的直径,AB=4,C为OA中点,D为半圆上一点,连CD,E为![]() 的中点,且CD∥BE,则CD的长为( )
的中点,且CD∥BE,则CD的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,由题意,可得△BHE≌△DHK,所以BE=KD=2x,EH=KH,由△KCO∽△EBO,可得![]() ,所以KO=1,KC=x,在Rt△BHE和Rt△BHO中,有BE2﹣EH2=BH2=BO2﹣OH2,即可得出x的值,进而得出CD的长.
,所以KO=1,KC=x,在Rt△BHE和Rt△BHO中,有BE2﹣EH2=BH2=BO2﹣OH2,即可得出x的值,进而得出CD的长.
解:如图,连接EO并延长与DC的延长线相交于点K,连接BD交OE于点H,
∵E为弧AD中点,
∴OE⊥AD,BH=DH,
∵BE∥CD,
∴∠EBH=∠KDH,∠E=∠K,
∴△BHE≌△DHK(AAS),
∴BE=KD=2x,EH=KH,
∵BE∥CD,
∴△KCO∽△EBO,
∴![]() ,
,
∵AB是半圆⊙O的直径,AB=4,C为OA的中点,
∴![]() ,
,
∴KO=1,KC=x,
∴KE=KO+OE=1+2=3,
∴EH=KH=1.5,OH=0.5,
∵BE2﹣EH2=BH2=BO2﹣OH2,
∴4x2﹣1.52=22﹣0.52,
解得:x![]() ,
,
∴CD=KD﹣KC=2x﹣x=x![]() ,
,
故选:B.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目