题目内容
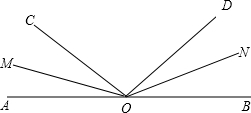 如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线.
如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD的平分线.(1)已知∠AOC=30°,∠BOD=60°,求∠MON的度数;
(2)如果只已知“∠COD=90°”,你能求出∠MON的度数吗?如果能,请求出;如果不能,请说明理由.
分析:(1)根据平角即可求得∠AOB的度数,再根据角平分线的定义求得∠AOM和∠BON的度数,从而求得∠MON的度数;
(2)因为OM、ON分别是∠AOC、∠BOD的平分线,故知∠MOC+∠NOD=
∠AOC+
∠BOD=
(∠AOC+∠BOD)即可解答.
(2)因为OM、ON分别是∠AOC、∠BOD的平分线,故知∠MOC+∠NOD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵∠AOB是平角,∠AOC=30°,∠BOD=60°,
∴∠COD=∠A0B-∠AOC-∠BOD=180-30-60=90°,
∵OM、ON分别是∠AOC、∠BOD的平分线,
∴∠MOC=
∠AOC=15°,∠NOD=
∠BOD=30°,
∴∠MON=∠MOC+∠COD+∠NOD=15+90+30=135°;
(2)能.
∵OM、ON分别是∠AOC、∠BOD的平分线.
∴∠MOC+∠NOD,
=
∠AOC+
∠BOD,
=
(∠AOC+∠BOD),
=
(180-90)=45°,
∴∠MON=∠MOC+∠NOD+∠COD=90+45=135°.
∴∠COD=∠A0B-∠AOC-∠BOD=180-30-60=90°,
∵OM、ON分别是∠AOC、∠BOD的平分线,
∴∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠MOC+∠COD+∠NOD=15+90+30=135°;
(2)能.
∵OM、ON分别是∠AOC、∠BOD的平分线.
∴∠MOC+∠NOD,
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∴∠MON=∠MOC+∠NOD+∠COD=90+45=135°.
点评:本题主要考查的计算的知识点,解答本题的突破口充分利用角平分线的知识点,本题难度不大.

练习册系列答案
相关题目
 18、如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF、FG、GH …添加钢管的长度都与OE相等,则最多能添加这样的钢管的根数为( )
18、如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF、FG、GH …添加钢管的长度都与OE相等,则最多能添加这样的钢管的根数为( ) 23、如图所示,∠AOB是平角,OC是射线,OD和OE分别是∠AOC,∠BOC的角平分线,你能求出∠DOE的度数吗?
23、如图所示,∠AOB是平角,OC是射线,OD和OE分别是∠AOC,∠BOC的角平分线,你能求出∠DOE的度数吗? 如图所示,∠AOB是平角,OC是射线,OD、OE分别是∠AOC、∠BOC的角平分线,若∠AOD=65°,求∠DOE和∠BOE的度数.
如图所示,∠AOB是平角,OC是射线,OD、OE分别是∠AOC、∠BOC的角平分线,若∠AOD=65°,求∠DOE和∠BOE的度数. 如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与0E相等,则最多能添加这样的钢管
如图所示,∠AOB是一个钢架,且∠AOB=10°,为了使钢架更加牢固,需在内部添加一些钢管EF,FG,GH,…,添加的钢管长度都与0E相等,则最多能添加这样的钢管