题目内容
【题目】如图,在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分…将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,则称∠BAC是△ABC的好角.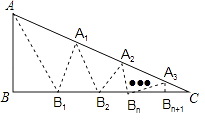
(1)若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C (设∠B>∠C)之间的等量关系为 .
(2)若一个三角形的最小角是4°,且该三角形的三个角均是此三角形的好角.请写出符合要求三角形的另两个角的度数 . (写出一种即可)
【答案】
(1)∠B=n∠C
(2)4、172;8、168;16、160;44、132;88°、88°
【解析】解:(1)∠B=3∠C;如图所示,

在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分,将余下部分沿∠B2A2C的平分线A2B3折叠,点B2与点C重合,则∠BAC是△ABC的好角.
证明如下:∵根据折叠的性质知,∠B=∠AA1B1,∠C=∠A2B2C,∠A1 B1C=∠A1A2B2,
∴根据三角形的外角定理知,∠A1A2B2=∠C+∠A2B2C=2∠C;
∵根据四边形的外角定理知,∠BAC+∠B+∠AA1B1﹣∠A1 B1C=∠BAC+2∠B﹣2∠C=180°,
根据三角形ABC的内角和定理知,∠BAC+∠B+∠C=180°,
∴∠B=3∠C;
由小丽展示的情形一知,当∠B=∠C时,∠BAC是△ABC的好角;
由小丽展示的情形二知,当∠B=2∠C时,∠BAC是△ABC的好角;
由小丽展示的情形三知,当∠B=3∠C时,∠BAC是△ABC的好角;
故若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C(不妨设∠B>∠C)之间的等量关系为∠B=n∠C;
所以答案是:.(2)由(1)知设∠A=4°,∵∠C是好角,∴∠B=4n°;
∵∠A是好角,∴∠C=m∠B=4mn°,其中m、n为正整数得4+4n+4mn=180
∴如果一个三角形的最小角是4°,三角形另外两个角的度数是4、172;8、168;16、160;44、132;88°、88°.
所以答案是:4、172;8、168;16、160;44、132;88°、88°
【考点精析】根据题目的已知条件,利用三角形的外角的相关知识可以得到问题的答案,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
【题目】每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
则这50名学生读数册数的众数、中位数是( )
A.3,3
B.3,2
C.2,3
D.2,2