题目内容
如图,将边长为an(n=1,2,3,…)的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次为A1,A2,A3,…,且后一个正方形的顶点在前一个正方形的中心,若第n个正方形纸片被第n+1个正方形纸片盖住部分的边长(即虚线的长度)记为bn,已知a1=1,an-an-1=2,则b1+b2+b3+…+bn=______.


过A1作A1A⊥EF于A,A1D⊥FG于D,
∵正方形EFGH,
∴∠A1AB=∠A1DC=∠EFG=90°,A1A=A1D,
∴∠AA1D=∠BA1C=90°,
∴∠AA1B=∠DAC,
∴△BAA1≌△CDA1,
∴AB=DC,
∵a1=1,an-an-1=2,
∴BF+FC=FA+FD=1,
同理第2个虚线之和是1+2=3,
同理第3个虚线之和是3+2=5,
同理第4个虚线之和是5+2=7
同理第5个虚线之和是7+2=9,
若摆放前n个(n为大于1的正整数)个正方形纸片,则图中被遮盖的线段(虚线部分)之和为:
1+3+5+…+(2n-1)=
×(1+2n-1)n=n2
故答案为:n2.
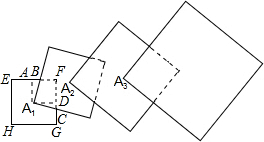
∵正方形EFGH,
∴∠A1AB=∠A1DC=∠EFG=90°,A1A=A1D,
∴∠AA1D=∠BA1C=90°,
∴∠AA1B=∠DAC,
∴△BAA1≌△CDA1,
∴AB=DC,
∵a1=1,an-an-1=2,
∴BF+FC=FA+FD=1,
同理第2个虚线之和是1+2=3,
同理第3个虚线之和是3+2=5,
同理第4个虚线之和是5+2=7
同理第5个虚线之和是7+2=9,
若摆放前n个(n为大于1的正整数)个正方形纸片,则图中被遮盖的线段(虚线部分)之和为:
1+3+5+…+(2n-1)=
| 1 |
| 2 |
故答案为:n2.


练习册系列答案
相关题目