题目内容
【题目】抛物线![]() (a ≠ 0)满足条件:(1)
(a ≠ 0)满足条件:(1)![]() ;(2)
;(2)![]() ;
;
(3)与x轴有两个交点,且两交点间的距离小于2.以下有四个结论:①![]() ;
;
②![]() ;③
;③![]() ;④
;④![]() ,其中所有正确结论的序号是
,其中所有正确结论的序号是
【答案】②④
【解析】
∵4a-b=0,∴抛物线的对称轴为x=-![]() =-2
=-2
∵a-b+c>0,∴当x=-1时,y>0,
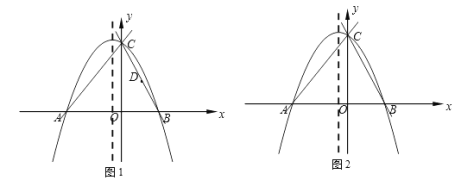
∵抛物线与x轴有两个不同的交点且这两个交点之间的距离小于2,
∴抛物线与x轴的两个交点的横坐标位于-3与-1之间,b2-4ac>0
∴16a2-4ac=4a(4a-c)>0,据条件得图象:

∴a>0,b>0,c>0,∴4a-c>0,∴4a>c即a>![]() ,
,
当x=-3时,9a-3b+c>0,由b=4a,∴c>3a即a<![]() ,∴
,∴![]() <a<
<a<![]() ,
,
当x=1时,y=a+b+c>0.故答案为:②,④.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目