题目内容
【题目】如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF.
(1)∠1=∠2吗?为什么?
(2)△ADE与△CDF全等吗?为什么?
(3)若AB=8cm,求四边形AEDF的面积.
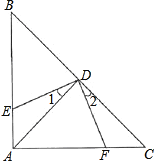
【答案】(1)相等,理由见解析;(2)全等,理由见解析;(3)16平方厘米.
【解析】试题分析:(1)利用公共角证明∠1=∠2.
(2)利用直角三角形斜边中线是斜边一半得到AD=CD,∠C=∠DAC, ∠1=∠2,利用ASA证明
△ADE与△CDF全等.
(3)利用(2)的结论,割补法,四边形面积恰好是等腰三角形面积一半.
(1)∵AB=AC,D是BC的中点,
∴∠ADC=90 ,
∴∠2+∠ADF=90,
∵DE⊥DF ,
∴∠1+∠ADF=90,
∴∠1=∠2 .
(2) ∵△ABC是等腰直角三角形,
∴∠C=45,
∵AB=AC,D是BC的中点.
∴∠DAC=∠DAE=45°,
∴DA=DC,
在△ADE与△CDF中,
∠EAD=∠C=45 , DA=DC , ∠1=∠2,
∴△ADE≌△CDF.
(3)由(2)△ADE≌△CDF,
∴S△AED=S△CDF,
∵S四边形AEDF=S△ADE+S△ADF,
∴S四边形AEDF=S△CDF+S△ADF =S△ADC,
= ![]() S△ABC,,
S△ABC,,
= ![]() ×8×8=16(㎝2).
×8×8=16(㎝2).

练习册系列答案
相关题目