Question

【题目】在中，，点为内一点.

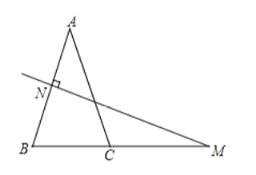
（1）如图1，连接，将沿射线方向平移，得到，点的对应点分别为点，连接.如果，，则 ．

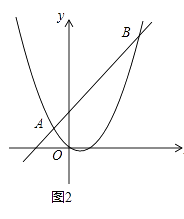
（2）如图2，连接，当时，求的最小值．

Answer 1

【答案】（1）；（2）2+2

【解析】

（1）连接CD，构造矩形ACBD和Rt△CDE，根据矩形的对角线相等以及勾股定理进行计算，即可求得CE的长；
（2）以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN，连接BN．根据△PAM、△ABN都是等边三角形，可得PA+PB+PC=CP+PM+MN，最后根据当C、P、M、N四点共线时，由CA=CB，NA=NB可得CN垂直平分AB，进而求得PA+PB+PC的最小值．

如图，连接CD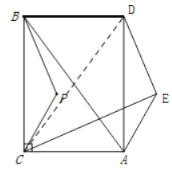

∵△BCP沿射线CA方向平移，得到△DAE，
∴BC∥AD且BC=AD，
∵∠ACB=90°，
∴四边形BCAD是矩形，
∴CD=AB=6，
∵BP=3，
∴DE=BP=3，
∵BP⊥CE，BP∥DE，
∴DE⊥CE，
∴在Rt△DCE中，CE=
（2）如图所示，以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN，连接BN．那么就将PA+PB+PC的值转化为CP+PM+MN的值，连接CN，当点P落在CN上时，PA+PB+PC的值最小．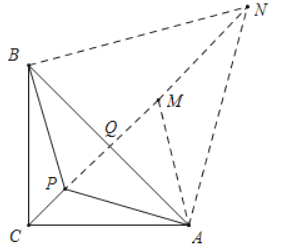

由旋转可得，△AMN≌△ABP，
∴MN=BP，PA=AM，∠PAM=60°=∠BAN，AB=AN，
∴△PAM、△ABN都是等边三角形，
∴PA=PM，
∴PA+PB+PC=CP+PM+MN，
当AC=BC=4时，AB=4，
当C、P、M、N四点共线时，由CA=CB，NA=NB可得CN垂直平分AB，
∴AQ=AB=2=CQ，NQ=AQ=2，
∴此时CN=CP+PM+MN=PA+PB+PC=2+2．