题目内容
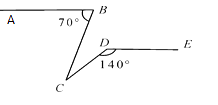
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE , ⑤CF=BD.正确的有( )个. 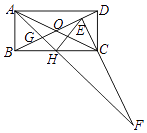
A.1
B.2
C.3
D.4
【答案】C
【解析】解:①在△BCE中,∵CE⊥BD,H为BC中点, ∴BC=2EH,又BC=2AB,
∴EH=AB,①正确;
②由①可知,BH=HE∴∠EBH=∠BEH,
又∠ABG+∠EBH=∠BEH+∠HEC=90°,
∴∠ABG=∠HEC,②正确;
③由AB=BH,∠ABH=90°,得∠BAG=45°,
同理:∠DHC=45°,∴∠EHC>∠DHC=45°,
∴△ABG≌△HEC,③错误;
④作AM⊥BD,则AM=CE,△AMD≌△CEB,
∵AD∥BC,
∴△ADG∽△HGB,
∴ ![]() =2,
=2,
即△ABG的面积等于△BGH的面积的2倍,
根据已知不能推出△AMG的面积等于△ABG的面积的一半,
即S△GAD≠S四边形GHCE ,
∴④错误
⑤∠ECH=∠CHF+∠F=45°+∠F,
又∠ECH=∠CDE=∠BAO,∠BAO=∠BAH+∠HAC,
∴∠F=∠HAC,
∴CF=BD,⑤正确.
正确的有3个.
故选C.
根据BC=2AB,H为BC中点,可得△ABH为等腰直角三角形,HE=BH=HC,可得△CEH为等腰三角形,又∠BCD=90°,CE⊥BD,利用互余关系得出角的相等关系,根据基本图形判断全等三角形,特殊三角形进行判断.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目