题目内容
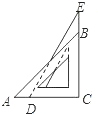 将一个含30°角的三角板和一个含45°角的三角板如图摆放,∠ACB与∠DCE完全重合,∠C=90°,∠A=45°,∠EDC=60°,AB=4
将一个含30°角的三角板和一个含45°角的三角板如图摆放,∠ACB与∠DCE完全重合,∠C=90°,∠A=45°,∠EDC=60°,AB=4| 2 |
分析:根据直角三角形的性质,求得BC,再求得EC,由此可以求出CE,再利用BE=CE-BC即可求出EB.
解答:解:在Rt△ABC中,
∵AB=4
,∠A=45°,
∴BC=4
×
=4
在Rt△EDC中,
∵∠EDC=60°,DE=6,
∴CE=DE•sin∠EDC=6×
=3
∴BE=CE-BC=3
-4.
故填空答案:3
-4.
∵AB=4
| 2 |
∴BC=4
| 2 |
| ||
| 2 |
在Rt△EDC中,
∵∠EDC=60°,DE=6,
∴CE=DE•sin∠EDC=6×
| ||
| 2 |
| 3 |
∴BE=CE-BC=3
| 3 |
故填空答案:3
| 3 |
点评:本题利用了直角三角形的性质和等腰三角形的性质求解.

练习册系列答案
相关题目
 将一个含30°角的三角板如图摆放,∠ACB与∠DCE完全重合.若AB=
将一个含30°角的三角板如图摆放,∠ACB与∠DCE完全重合.若AB= 如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是( )
如图,将一个含30°角的三角板的直角顶点放在直尺的一边上,如果∠1=115°,那么∠2的度数是( ) ,DE=6,则EB= .
,DE=6,则EB= .
 ,DE=6,则EB=
.
,DE=6,则EB=
.