题目内容
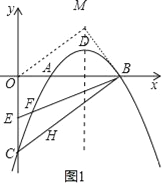
【题目】如图，在平面直角坐标系中，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A（1，0），B（3，0）两点，与y轴交于点C，其顶点为点D，点E的坐标为（0，﹣1），该抛物线与BE交于另一点F，连接BC．
（1）求该抛物线的解析式；
（2）一动点M从点D出发，以每秒1个单位的速度沿与y轴平行的方向向上运动，连接OM，BM，设运动时间为t秒（t＞0），在点M的运动过程中，当t为何值时，∠OMB=90°？
（3）在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，请直接写出点P的坐标；若不存在，请说明理由．
【答案】（1）y=﹣
x2+
x﹣2；（2）
﹣
；（3）P（
， 
）．
【解析】（1）用待定系数法求出抛物线解析式；
（2）设出点M，用勾股定理求出点M的坐标，从而求出MD，最后求出时间t；
（3）由∠PBF被BA平分，确定出过点B的直线BN的解析式，求出此直线和抛物线的交点即可．
解：（1）∵抛物线y=ax2+bx﹣2（a≠0）与x轴交于A（1，0）、B（3，0）两点，
∴
，
∴
，
∴抛物线解析式为y=﹣
x2+
x﹣2；
（2）如图1，
由（1）知y=﹣
x2+
x﹣2=﹣
（x﹣2）2+
；
∵D为抛物线的顶点，
∴D（2， 
），
∵一动点M从点D出发，以每秒1个单位的速度平沿行与y轴方向向上运动，
∴设M（2，m），（m＞
），
∴OM2=m2+4，BM2=m2+1，OB2=9，
∵∠OMB=90°，
∴OM2+BM2=OB2，
∴m2+4+m2+1=9，
∴m=
或m=﹣
（舍），
∴M（0， 
），
∴MD=
﹣
，
∵一动点M从点D出发，以每秒1个单位的速度平沿行与y轴方向向上运动，
∴t=
﹣；
（3）存在点P，使∠PBF被BA平分，
如图2，
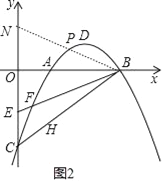
∴∠PBO=∠EBO，
∵E（0，﹣1），
∴在y轴上取一点N（0，1），
∵B（3，0），
∴直线BN的解析式为y=﹣
x+1①，
∵点P在抛物线y=﹣
x2+
x﹣2②上，
联立①②得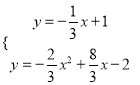
，
解得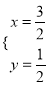
或
（舍去），
∴P（
， 
）．
“点睛”本题看考查二次函数综合题、待定系数法、一次函数的应用、三角形的面积角平分线等知识，解题时根据灵活运用所学知识，学会构建一次函数，利用方程组求两个函数交点坐标，属于中考常考题型.
