题目内容
函数y=ax+b和y=ax2+bx+c（a≠0）在同一个坐标系中的图象可能为
- A.
- B.
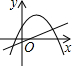
- C.
- D.
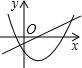
D
分析：本题可先由一次函数y=ax+b图象得到字母系数的正负，再与二次函数ax2+bx+c的图象相比较看是否一致．
解答：B、C中，由二次函数图象开口方向得到a的符号，与由一次函数的图象得到a的符号，两者相矛盾，排除B、C；
A、D中，由抛物线图象可知，开口向上，a＞0，对称轴x=-
＞0，b＜0；而选项A由一次函数的图象可知a＞0 b＞0，
两者相矛盾，排除A．
只有D正确．
故选D．
点评：解决此类问题步骤一般为：（1）根据图象的特点判断a取值是否矛盾；（2）根据二次函数图象判断其顶点坐标是否符合要求．
分析：本题可先由一次函数y=ax+b图象得到字母系数的正负，再与二次函数ax2+bx+c的图象相比较看是否一致．
解答：B、C中，由二次函数图象开口方向得到a的符号，与由一次函数的图象得到a的符号，两者相矛盾，排除B、C；
A、D中，由抛物线图象可知，开口向上，a＞0，对称轴x=-
＞0，b＜0；而选项A由一次函数的图象可知a＞0 b＞0，两者相矛盾，排除A．
只有D正确．
故选D．
点评：解决此类问题步骤一般为：（1）根据图象的特点判断a取值是否矛盾；（2）根据二次函数图象判断其顶点坐标是否符合要求．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
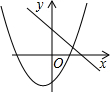
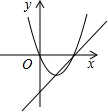
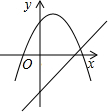
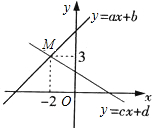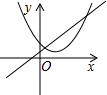
如图，已知函数y=ax+b和y=cx+d的图象交于点M，则根据图象可知，关于x，y的二元一次方程组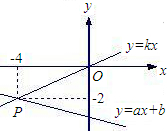
如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于x，y的二元一次方程组