题目内容
若y=(m-2)x+(m2-4)是正比例函数,则m的取值是
| A.2 | B.-2 | C.±2 | D.任意实数 |
B
分析:由正比例函数的定义可得m2-4=0,且2-m≠0,然后解关于m的一元二次方程即可.
解答:解:由正比例函数的定义可得:m2-4=0,且2-m≠0,
解得,m=-2;
故答案是:B.
点评:本题考查了正比例函数的定义.解题关键是掌握正比例函数的定义条件:正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.
解答:解:由正比例函数的定义可得:m2-4=0,且2-m≠0,
解得,m=-2;
故答案是:B.
点评:本题考查了正比例函数的定义.解题关键是掌握正比例函数的定义条件:正比例函数y=kx的定义条件是:k为常数且k≠0,自变量次数为1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
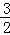 x+3
x+3 x+3
x+3 ②
② ③
③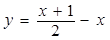
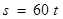 ⑤
⑤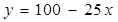
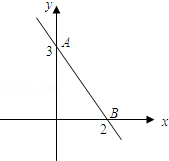
 的图象如图,则下列结
的图象如图,则下列结  <0;②
<0;② >0;③
>0;③ >0;④当
>0;④当 <3时,
<3时, <
<

 经过点
经过点 和
和 轴正半轴上的一点,如果
轴正半轴上的一点,如果 (为坐标原点)的面积为2,则
(为坐标原点)的面积为2,则 的值为 .
的值为 .