题目内容
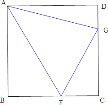
【题目】(1)如图,在正方形 ABCD 中,∠FAG=45°,请直接写出 DG,BF 与FG 的数量关系,不需要证明.
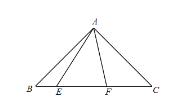
(2)如图,在 Rt△ABC 中,∠BAC=90°,AB=AC,E,F 分别是 BC 上两点,∠EAF=45°,
①写出 BE,CF,EF 之间的数量关系,并证明.
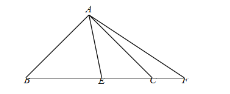
②若将(2)中的△AEF 绕点 A 旋转至如图所示的位置,上述结论是否仍然成立? 若不成立,直接写出新的结论 ,无需证明.
(3)如图,△AEF 中∠EAF=45°,AG⊥EF 于 G,且GF=2,GE=3,则 ![]() = .
= .
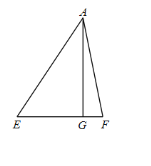
【答案】(1)FG=BF+DG;(2)①EF2=BE2+FC2,理由见解析;②仍然成立;(3)15
【解析】
(1)把△AGD绕点A逆时针旋转90°至△ABP,可使AD与AB重合,再证明△AFG≌△AFP进而得到PF=FG,即可得FG=BF+DG;
(2)①根据△AFC绕点A顺时针旋转90°得到△AGB,根据旋转的性质,可知△ACF≌△ABG得到BG=FC,AG=AF,∠C=∠ABG,∠FAC=∠GAB,根据Rt△ABC中的AB=AC得到∠GBE=90°,所以GB2+BE2=GE2,证△AGE≌△AFE,利用EF=EG得到EF2=BE2+FC2;
②将△ABE绕点A逆时针旋转使得AB与AD重合,点E的对应点是G,同上的方法证得GC2+CF2=FG2,再设法利用SAS证得△AFG≌△AFE即可求解;
(3)将△AEG沿AE对折成△AEB,将△AFG沿AF对折成△AFD,延长BE、DF相交于C,构成正方形ABCD,在Rt△EFC中,利用勾股定理求得正方形的边长,即可求得AG的长,从而求得答案.
(1)∵四边形ABCD为正方形,
∴AB=AD,∠ADC=∠ABC=90°,
∴把△AGD绕点A逆时针旋转90°至△ABP,使AD与AB重合,
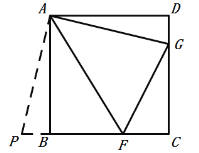
∴∠BAP=∠DAG,AP= AG,
∵∠BAD=90°,∠FAG=45°,
∴∠BAF+∠DAG=45°,
∴∠PAF=∠FAG=45°,
∵∠ADC=∠ABC=90°,
∴∠FBP=180°,点F、B、P共线,
在△AFG和△AFP中,
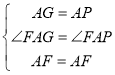 ,
,
∴△AFG≌△AFP(SAS),
∴PF=FG,
即:FG=BF+DG;
(2)①FC2+BE2=EF2,证明如下:
∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
将△AFC绕点A顺时针旋转90°得到△AGB,
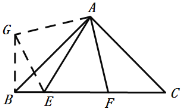
∴△ACF≌△ABG,
∴BG=FC,AG=AF,∠C=∠ABG=45°,∠FAC=∠GAB,
∴∠GBE=∠ABG +∠ABC =90°,
∴GB2+BE2=GE2,
又∵∠EAF=45°,
∴∠BAE+∠FAC=45°,
∴∠GAB+∠BAE=45°,
即∠GAE=45°,
在△AGE和△AFE中,
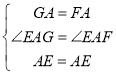 ,
,
∴△AGE≌△AFE(SAS),
∴GE=EF,
∴FC2+BE2=EF2;
②仍然成立,理由如下:
如图,将△ABE绕点A逆时针旋转使得AB与AD重合,点E的对应点为点G,
∴△ACG≌△ABE,
∴CG=BE,AG=AE,∠ACG=∠ABE=45°,∠BAE=∠CAG,
∴∠GCB=∠ACB +∠ACG =90°,即∠GCF=90°,
∴GC2+CF2=FG2,
∵∠BAE+∠EAC=∠BAC=90°,
∴∠CAG+∠EAC=90°,
又∵∠EAF=45°,
∴∠GAF=90°-∠EAF=45°,
∴∠GAF=∠EAF=45°,
在△AFG和△AFE中,
 ,
,
∴△AFG≌△AFE(SAS),
∴GF=EF,
∴FC2+BE2=EF2;

(3)将△AEG沿AE对折成△AEB,将△AFG沿AF对折成△AFD,延长BE、DF相交于C,
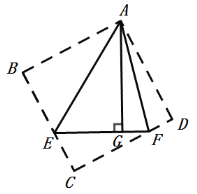
∴△AEG![]() △AEB,△AFG
△AEB,△AFG![]() △AFD,
△AFD,
∴AB=AG=AD,BE=EG=3,DF=FG=2,∠EAG=∠EAB,∠FAG=∠FAD,∠B=∠D=90°,
∵∠EAF=45°,
∴∠EAB+∠FAD=∠EAG+∠FAG=∠EAF=45°,
∴∠BAD=90°,
∴四边形ABCD为正方形,
设AG =![]() ,则AB=BC=CD=
,则AB=BC=CD=![]() ,
,
在Rt△EFC中,EF=3+2=5,EC=BC-BE=![]() ,FC=CD-DF=
,FC=CD-DF=![]() ,
,
∴![]() ,
,
故![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴AG=6,
∴![]() .
.
故答案为:15.