题目内容
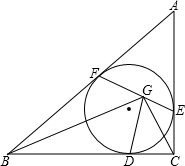 △ABC的内切圆分别切BC、CA、AB三边于D、E、F,G是EF上的一点,且DG⊥EF,求证:DG平分∠BGC.
△ABC的内切圆分别切BC、CA、AB三边于D、E、F,G是EF上的一点,且DG⊥EF,求证:DG平分∠BGC.
分析:连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK.则Rt△BFN∽Rt△DEG,Rt△CEK∽Rt△DFG,从而证得
=
,于是△BFG∽△CEG,所以∠BGD=∠CGD.即DG平分∠BGC.
| BF |
| CE |
| FG |
| GE |
解答: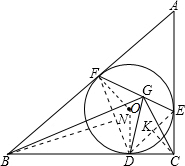 证明:连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK,OF,OD.则:
证明:连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK,OF,OD.则:
∵△ABC的内切圆分别切BC、CA、AB三边于D、E、F,
∴BF=BD,CD=CE,
∴BN⊥DF,CK⊥DE,∠FBN=
∠FBD,
∵∠DOF=2∠E,∠DOF+∠FBD=180°,∠GDE+∠E=90°,
∴∠FBN=∠EDG,
∵DG⊥EG,
∴∠BNF=∠DGE=90°,
∴Rt△BFN∽Rt△DEG,
=
=
(2分)
同理:Rt△CEK∽Rt△DFG,
=
=
(2分)
∴BF•GE=
DF•DE=CE•FG(4分)
∴
=
,而∠BFG=∠CEG(2分)
∴△BFG∽△CEG,于是∠BGF=∠CGE.
∵DG⊥EF,∴∠BGD=∠CGD.
即DG平分∠BGC.
 证明:连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK,OF,OD.则:
证明:连接DF、DE,设N、K分别是DF、DE的中点,连接BN、CK,OF,OD.则:∵△ABC的内切圆分别切BC、CA、AB三边于D、E、F,
∴BF=BD,CD=CE,
∴BN⊥DF,CK⊥DE,∠FBN=
| 1 |
| 2 |
∵∠DOF=2∠E,∠DOF+∠FBD=180°,∠GDE+∠E=90°,
∴∠FBN=∠EDG,
∵DG⊥EG,
∴∠BNF=∠DGE=90°,
∴Rt△BFN∽Rt△DEG,
| BF |
| DE |
| FN |
| GE |
| FD |
| 2GE |
同理:Rt△CEK∽Rt△DFG,
| CE |
| DF |
| EK |
| FG |
| ED |
| 2FG |
∴BF•GE=
| 1 |
| 2 |
∴
| BF |
| CE |
| FG |
| GE |
∴△BFG∽△CEG,于是∠BGF=∠CGE.
∵DG⊥EF,∴∠BGD=∠CGD.
即DG平分∠BGC.
点评:本题考查了三角形的内切圆和相似三角形的判定和性质.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
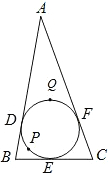 如图,△ABC的内切圆分别切
如图,△ABC的内切圆分别切
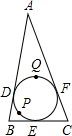 如图,△ABC的内切圆分别切AB、BC、AC于D、E、F三点,其中P、Q两点分别在
如图,△ABC的内切圆分别切AB、BC、AC于D、E、F三点,其中P、Q两点分别在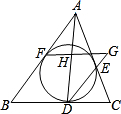 如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.
如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.