题目内容
【题目】已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点E在BC上,取DF的中点G,连结EG、CG.
(1)请添加一条辅助线,构造一个和△FEG全等的三角形,并证明它们全等.
(2)探索EG、CG的数量关系和位置关系,并证明.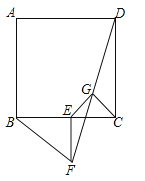
【答案】解:(1)延长EG交CD于点H,如图,则△DHG≌△FEG.证明如下:
∵∠BEF=90°,
∴EF⊥BC,
而CD⊥BC,
∴EF∥CD,
∴∠1=∠2,
∵点G为DF的中点,
∴DG=FG,
在△DHG和△FEG中, ,
,
∴△DHG≌△FEG(ASA);
(2)EG=CG,EG⊥CG.证明如下:
∵△DHG≌△FEG,
∴EF=DH,EG=HG,
∵BE=EF,
∴BE=DH,
∵CB=CD,
∴CD﹣DH=CB﹣BE,即CH=CE,
∴△CHE为等腰直角三角形,
∵EG=GH,
∴CG⊥EH,CG=EG=GH,
即EG=CG,EG⊥CG.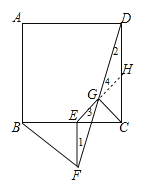
【解析】(1)延长EG交CD于点H,如图,先证明EF∥CD,则∠1=∠2,再由点G为DF的中点得到DG=FG,然后利用“ASA”判断△DHG≌△FEG;
(2)由△DHG≌△FEG得到EF=DH,EG=HG,而BE=EF,所以BE=DH,根据正方形的性质得CB=CD,则CH=CE,于是可判断△CHE为等腰直角三角形,然后根据等腰直角三角形的性质得到CG⊥EH,CG=EG=GH,即EG=CG,EG⊥CG.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案